
【题目】如图,已知点![]() 是
是![]() 外一点,直线
外一点,直线![]() 与
与![]() 相切于点
相切于点![]() ,直线
,直线![]() 分别交
分别交![]() 于点
于点![]() 、
、![]() ,
,![]() ,
,![]() 交
交![]() 于点
于点![]() .
.
(1)求证:![]() ;
;
(2)当![]() 的半径为
的半径为![]() ,
,![]() 时,求
时,求![]() 的长.
的长.
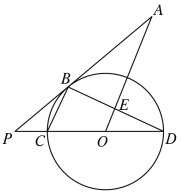
【答案】(1)证明见解析;(2)21.
【解析】
(1)连接OB,由切线的性质可得OB⊥PA,然后根据直径所对的圆周角为直角得到∠CBD=90°,再根据等角的余角相等推出∠BCD=∠BOA,由等量代换得到∠CBO=∠BOA,即可证平行;
(2)先由勾股定理求出BD,然后由垂径定理得到DE,求出OE,再利用△ABE∽△DOE的对应边成比例,即可求出AE.
(1)如图,连接OB,
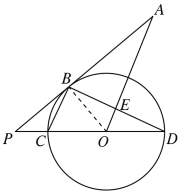
∵直线PA与![]() 相切于点B,
相切于点B,
∴OB⊥PA,
∴∠PAO+∠BOA=90°
∵CD是![]() 的直径
的直径
∴∠CBD=90°,∠PDB+∠BCD=90°
又∵∠PAO=∠PDB
∴∠BOA=∠BCD
∵OB=OC
∴∠BCD=∠CBO
∴∠CBO=∠BOA
∴OA∥BC
(2)∵半径为10,![]() ,
,
∴BD=![]()
由(1)可知∠CBD=90°,OA∥BC
∴OE⊥BD
∴![]() 是
是![]() 的中点,DE=
的中点,DE=![]() BD=
BD=![]()
∴![]()
∵![]() ,
,![]()
∴![]() ,
,
∴![]() ,即
,即![]()
∴![]() .
.


科目:初中数学 来源: 题型:
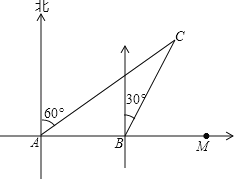
【题目】如图,某货船以24海里/时的速度将一批重要物资从A处运往正东方向的M处,在点A处测得某岛C在北偏东60°的方向上.该货船航行30分钟后到达B处,此时再测得该岛在北偏东30°的方向上,
(1)求B到C的距离;
(2)如果在C岛周围9海里的区域内有暗礁.若继续向正东方向航行,该货船有无触礁危险?试说明理由(![]() ≈1.732).
≈1.732).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() 是线段
是线段![]() 延长线上一点,连接
延长线上一点,连接![]() ,过点
,过点![]() 作
作![]() 于
于![]() .
.

(1)求证:![]() .
.
(2)将射线![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 后,所得的射线与线段
后,所得的射线与线段![]() 的延长线交于点
的延长线交于点![]() ,连接
,连接![]() .
.
①依题意补全图形;
②用等式表示线段![]() ,
,![]() ,
,![]() 之间的数量关系,并证明.
之间的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程kx2﹣2(k+1)x+k﹣1=0有两个不相等的实数根.
(1)求k的取值范围.
(2)是否存在实数k,使此方程的两个实数根的倒数和等于1?若存在,求出k的值:若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 的对称轴为直线
的对称轴为直线![]() ,该抛物线与
,该抛物线与![]() 轴的两个交点分别为
轴的两个交点分别为![]() 和
和![]() ,与
,与![]() 轴的交点为
轴的交点为![]() ,其中
,其中![]() .
.
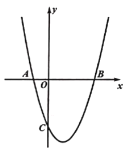
(1)写出点![]() 的坐标________;
的坐标________;
(2)若抛物线上存在一点![]() ,使得
,使得![]() 的面积是
的面积是![]() 的面积的
的面积的![]() 倍,求点
倍,求点![]() 的坐标;
的坐标;
(3)点![]() 是线段
是线段![]() 上一点,过点
上一点,过点![]() 作
作![]() 轴的垂线交抛物线于点
轴的垂线交抛物线于点![]() ,求线段
,求线段![]() 长度的最大值.
长度的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在6×8的网格中,每个小正方形的边长均为1,点O和△ABC的顶点均为小正方形的顶点.

(1)在图中△ABC的内部作△A′B′C′,使△A′B′C′和△ABC位似,且位似中心为点O,位似比为1:2;
(2)连接(1)中的AA′,则线段AA′的长度是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(阅读)
辅助线是几何解题中沟通条件与结论的桥梁.在众多类型的辅助线中,辅助圆作为一条曲线型辅助线,显得独特而隐蔽.
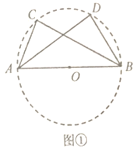
性质:如图①,若![]() ,则点
,则点![]() 在经过
在经过![]() ,
,![]() ,
,![]() 三点的圆上.
三点的圆上.
(问题解决)
运用上述材料中的信息解决以下问题:
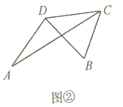
(1)如图②,已知![]() .求证:
.求证:![]() .
.
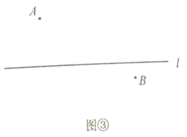
(2)如图③,点![]() ,
,![]() 位于直线
位于直线![]() 两侧.用尺规在直线
两侧.用尺规在直线![]() 上作出点
上作出点![]() ,使得
,使得![]() .(要求:要有画图痕迹,不用写画法)
.(要求:要有画图痕迹,不用写画法)
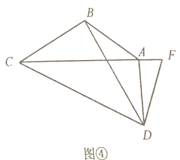
(3)如图④,在四边形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 在
在![]() 的延长线上,连接
的延长线上,连接![]() ,
,![]() .求证:
.求证:![]() 是
是![]() 外接圆的切线.
外接圆的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
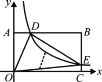
【题目】如图,在以O为原点的直角坐标系中,矩形OABC的两边OC、OA分别在x轴、y轴的正半轴上,反比例函数![]() (x>0)与AB相交于点D,与BC相交于点E,若BD=3AD,且△ODE的面积是9,则k的值是( )
(x>0)与AB相交于点D,与BC相交于点E,若BD=3AD,且△ODE的面积是9,则k的值是( )
A.![]() B.
B.![]() C.
C.![]() D.12
D.12
查看答案和解析>>
科目:初中数学 来源: 题型:
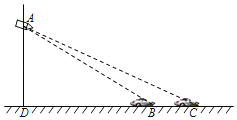
【题目】如图,一辆轿车在经过某路口的感应线B和C处时,悬臂灯杆上的电子警察拍摄到两张照片,两感应线之间距离BC为6m,在感应线B、C两处测得电子警察A的仰角分别为∠ABD=18°,∠ACD=14°.求电子警察安装在悬臂灯杆上的高度AD的长.
(参考数据:sin14°≈0.242,cos14°≈0.97,tan14°≈0.25,sin18°≈0.309,cos18°≈0.951,tan18°≈0.325)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com