
【题目】抛物线![]() 的对称轴为直线
的对称轴为直线![]() ,该抛物线与
,该抛物线与![]() 轴的两个交点分别为
轴的两个交点分别为![]() 和
和![]() ,与
,与![]() 轴的交点为
轴的交点为![]() ,其中
,其中![]() .
.
(1)写出点![]() 的坐标________;
的坐标________;
(2)若抛物线上存在一点![]() ,使得
,使得![]() 的面积是
的面积是![]() 的面积的
的面积的![]() 倍,求点
倍,求点![]() 的坐标;
的坐标;
(3)点![]() 是线段
是线段![]() 上一点,过点
上一点,过点![]() 作
作![]() 轴的垂线交抛物线于点
轴的垂线交抛物线于点![]() ,求线段
,求线段![]() 长度的最大值.
长度的最大值.
【答案】(1)![]() ;(2)点
;(2)点![]() 的坐标为
的坐标为![]() 或
或![]() ;(3)MD长度的最大值为
;(3)MD长度的最大值为![]() .
.
【解析】
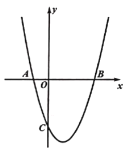
(1)抛物线的对称轴为x=1,点A坐标为(-1,0),则点B(3,0),即可求解;
(2)由S△POC=2S△BOC,则x=±2OB=6,即可求解;
(3)设:点M坐标为(x,x-3),则点D坐标为(x,x2-2x-3),则MD=x-3-x2+2x+3,即可求解.
解:(1)抛物线的对称轴为![]() ,点
,点![]() 坐标为
坐标为![]() ,则点
,则点![]() ,
,
故:答案为![]() ;
;
(2)二次函数表达式为:![]() ,
,
即:![]() ,解得:
,解得:![]() ,
,
故抛物线的表达式为:![]() ,
,
所以![]()
由题意得:![]() ,
,
设P(x, ![]() )
)
则![]()
所以![]() 则
则![]() ,
,
所以当![]() 时,
时,![]() =-21,当
=-21,当![]() 时,
时,![]() =45
=45
故点![]() 的坐标为
的坐标为![]() 或
或![]() ;
;
(3)如图所示,
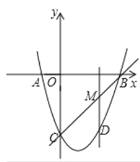
将点![]() 坐标代入一次函数
坐标代入一次函数![]() 得表达式得
得表达式得
![]() ,解得:
,解得:![]() ,
,
故直线![]() 的表达式为:
的表达式为:
![]() ,
,
设:点![]() 坐标为
坐标为![]() ,则点
,则点![]() 坐标为
坐标为![]() ,
,
则![]() ,
,
故MN长度的最大值为![]() .
.


科目:初中数学 来源: 题型:
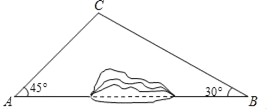
【题目】为加快城乡对接,建设全域美丽乡村,某地区对A、B两地间的公路进行改建.如图,A、B两地之间有一座山,汽车原来从A地到B地需途径C地沿折线ACB行驶,现开通隧道后,汽车可直接沿直线AB行驶.已知BC=80千米,∠A=45°,∠B=30°.
(1)开通隧道前,汽车从A地到B地大约要走多少千米?
(2)开通隧道后,汽车从A地到B地大约可以少走多少千米?(结果精确到0.1千米)(参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
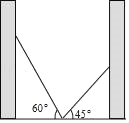
【题目】如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左侧墙上与地面成60°角时,梯子顶端距离地面2![]() 米,若保持梯子底端位置不动,将梯子斜靠在右端时,与地面成45°,则小巷的宽度为_____米(结果保留根号).
米,若保持梯子底端位置不动,将梯子斜靠在右端时,与地面成45°,则小巷的宽度为_____米(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
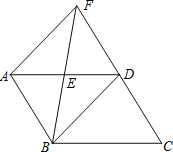
【题目】如图,ABCD中,E为AD的中点,直线BE、CD相交于点F.连接AF、BD.
(1)求证:AB=DF;
(2)若AB=BD,求证:四边形ABDF是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
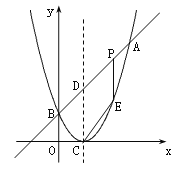
【题目】如图,已知二次函数图象的顶点坐标为C(1,0),直线![]() 与该二次函数的图象交于A、B两点,其中A点的坐标为(3,4),B点在轴
与该二次函数的图象交于A、B两点,其中A点的坐标为(3,4),B点在轴![]() 上.
上.
(1)求![]() 的值及这个二次函数的关系式;
的值及这个二次函数的关系式;
(2)P为线段AB上的一个动点(点P与A、B不重合),过P作![]() 轴的垂线与这个二次函数的图象交于点E点,设线段PE的长为
轴的垂线与这个二次函数的图象交于点E点,设线段PE的长为![]() ,点P的横坐标为
,点P的横坐标为![]() ,求
,求![]() 与
与![]() 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
(3)D为直线AB与这个二次函数图象对称轴的交点,在线段AB上是否存在一点P,使得四边形DCEP是平行四边形?若存在,请求出此时P点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019新型冠状病毒,因武汉病毒性肺炎病例而被发现,2020年1月12日被世界卫生组织命名“2019-nCoV”.冠状病毒是一个大型病毒家族,借助电子显微镜,我们可以看到这些病毒直径约为125纳米(1纳米=1 ![]() 10-9米),125纳米用科学记数法表示等于( )米
10-9米),125纳米用科学记数法表示等于( )米
A.1.25![]() 10-10B.1.25
10-10B.1.25![]() 10-11C.1.25
10-11C.1.25 ![]() 10-8D.1.25
10-8D.1.25![]() 10-7
10-7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,有一个可以自由转动的转盘,其盘面分为4等份,在每一等份分别标有对应的数字2,3,4,5.小明打算自由转动转盘10次,现已经转动了8次,每一次停止后,小明将指针所指数字记录如下:
次数 | 第1次 | 第2次 | 第3次 | 第4次 | 第5次 | 第6次 | 第7次 | 第8次 | 第9次 | 第10次 |
数字 | 3 | 5 | 2 | 3 | 3 | 4 | 3 | 5 |
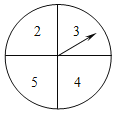
(1)求前8次的指针所指数字的平均数.
(2)小明继续自由转动转盘2次,判断是否可能发生“这10次的指针所指数字的平均数不小于3.3,且不大于3.5”的结果?若有可能,计算发生此结果的概率,并写出计算过程;若不可能,说明理由.(指针指向盘面等分线时为无效转次.)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某中学艺术节期间,向学校学生征集书画作品.九年级美术李老师从全年级14个班中随机抽取了A、B、C、D四个班,对征集到的作品的数量进行了分析统计,制作了如下两幅不完整的统计图.
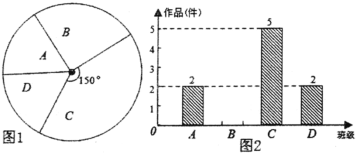
(1)李老师采取的调查方式是______________(填“普查”或“抽样调查”),李老师所调查的4个班征集到作品共_________件,其中B班征集到作品_______________件.
(2)如果全年级参展作品中有4件获得一等奖,其中有2名作者是男生,2名作者是女生.现在要抽取两人去参加学校总结表彰座谈会,求恰好抽中一男一女的概率.(要求用树状图或列表法写出分析过程).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com