
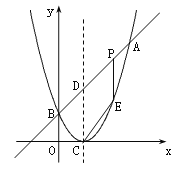
【题目】如图,已知二次函数图象的顶点坐标为C(1,0),直线![]() 与该二次函数的图象交于A、B两点,其中A点的坐标为(3,4),B点在轴
与该二次函数的图象交于A、B两点,其中A点的坐标为(3,4),B点在轴![]() 上.
上.
(1)求![]() 的值及这个二次函数的关系式;
的值及这个二次函数的关系式;
(2)P为线段AB上的一个动点(点P与A、B不重合),过P作![]() 轴的垂线与这个二次函数的图象交于点E点,设线段PE的长为
轴的垂线与这个二次函数的图象交于点E点,设线段PE的长为![]() ,点P的横坐标为
,点P的横坐标为![]() ,求
,求![]() 与
与![]() 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
(3)D为直线AB与这个二次函数图象对称轴的交点,在线段AB上是否存在一点P,使得四边形DCEP是平行四边形?若存在,请求出此时P点的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)存在,P点坐标为(2,3).
;(3)存在,P点坐标为(2,3).
【解析】
试题(1)、将点A代入直线解析式求出m的值,将二次函数设出顶点式,然后求出函数解析式;(2)、分别得出点P和点E的纵坐标,然后将两点的纵坐标做差得出h与x的函数关系式;(3)、根据平行四边形性质可得:PE=DC,根据点D在直线y=x+1上得出点D的坐标,从而得出方程求出x的值,得出点P的坐标.
试题解析:(1)、∵点A(3,4)在直线y=x+m上,∴4=3+m. ∴m=1.
设所求二次函数的关系式为y=a(x-1)2. ∵点A(3,4)在二次函数y=a(x-1)2的图象上,
∴4=a(3-1)2, ∴a=1. ∴所求二次函数的关系式为y=(x-1)2.即y=x2-2x+1.
(2)、设P、E两点的纵坐标分别为yP和yE∴PE=h=yP-yE=(x+1)-(x2-2x+1)=-x2+3x.
即h=-x2+3x(0<x<3).
(3)、存在.要使四边形DCEP是平行四边形,必需有PE=DC.∵点D在直线y=x+1上,
∴点D的坐标为(1,2),∴-x2+3x=2.即x2-3x+2=0. 解得:x1=2,x2=1(不合题意,舍去)
∴当P点的坐标为(2,3)时,四边形DCEP是平行四边形.


科目:初中数学 来源: 题型:
【题目】如图将小球从斜坡的O点抛出,小球的抛出路线可以用二次函数y=ax2+bx刻画,顶点坐标为(4,8),斜坡可以用y=![]() x刻画.
x刻画.
(1)求二次函数解析式;
(2)若小球的落点是A,求点A的坐标;
(3)求小球飞行过程中离坡面的最大高度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国家规定“中小学生每天在校体育活动时间不低于1小时”.为此,某市就“你每天在校体育活动时间是多少”的问题随机调查了辖区内300名初中学生.根据调查结果绘制成的统计图(部分)如图所示,其中分组情况是:
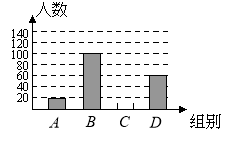
A组:![]() ;B组:
;B组:![]()
C组:![]() D组:
D组:![]()
请根据上述信息解答下列问题:
(1)C组的人数是;
(2)本次调查数据的中位数落在组内;
(3)若该辖区约有24 000名初中学生,请你估计其中达国家规定体育活动时间的人约有多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+2与x轴相交于A(﹣1,0),B(4,0)两点,与y轴相交于点C.
(1)求抛物线的解析式;
(2)将△ABC绕AB中点M旋转180°,得到△BAD.
①求点D的坐标;
②判断四边形ADBC的形状,并说明理由;
(3)在该抛物线对称轴上是否存在点P,使△BMP与△BAD相似?若存在,请求出所有满足条件的P点的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象如图所示,则下列结论中:①ac>0;②a+b+c<0;③4a﹣2b+c<0;④2a+b<0;⑤4ac﹣b2<4a;⑥a+b>0中,其中正确的个数为( )
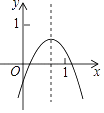
A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一段抛物线:y=﹣x(x﹣5)(0≤x≤5),记为C1,它与x轴交于点O,A1;将C1绕点A1旋转180°得C2,交x轴于点A2;将C2绕点A2旋转180°得C3,交x轴于点A3;…如此进行下去,得到一“波浪线”,若点P(2018,m)在此“波浪线”上,则m的值为( )

A. 4 B. ﹣4 C. ﹣6 D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
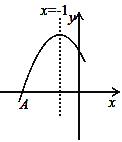
【题目】如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(﹣3,0),对称轴为直线x=﹣1,给出以下结论:①abc<0 ②b2﹣4ac>0 ③4b+c<0 ④若B(﹣![]() ,y1)、C(﹣
,y1)、C(﹣![]() ,y2)为函数图象上的两点,则y1>y2⑤当﹣3≤x≤1时,y≥0,
,y2)为函数图象上的两点,则y1>y2⑤当﹣3≤x≤1时,y≥0,
其中正确的结论是(填写代表正确结论的序号)__________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小清为班级办黑板报时遇到一个难题,在版面设计过程中需要将一个半圆三等分,小华帮他设计了一个尺规作图的方法.
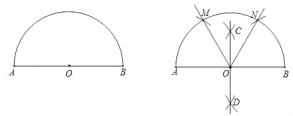
小华的作法如下:
(1)作AB的垂直平分线CD交AB于点O;
(2)分别,以A、B为圆心,以AO(或BO)的长为半径画弧,分别交半圆于点M、N;
(3)连接OM、ON即可
请根据该同学的作图方法完成以下推理:
∵半圆AB
∴ 是直径.
∵CD是线段AB的垂直平分线
∴OA=OB(依据: )
∵OA=OM=
∴△OAM为等边三角形(依据: )
∴∠AOM=60°(依据: )
同理可得∠BON=60°
∠AOM=∠BON=∠MON=60°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象与反比例函数y=![]() 的图象交于A(﹣2,1),B(1,n)两点.
的图象交于A(﹣2,1),B(1,n)两点.
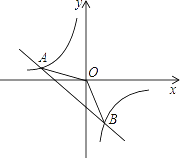
(1)试确定上述反比例函数和一次函数的表达式;
(2)求△AOB的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com