
【题目】如图,MN是正方形ABCD的一条对称轴,点P是直线MN上的一个动点当PC+PD最小时,∠PCD=( )°. 
A.60°
B.45°
C.30°
D.15°
【答案】B
【解析】解:连接BD交MN于P′,如图,
∵MN是正方形ABCD的一条对称轴,
∴P′B=P′C,
∴P′C+P′D=P′B+P′D=BD,
∴此时P′C+P′D最短,即点P运动到P′位置时,PC+PD最小,
∵点P′为正方形的对角线的交点,
∴∠P′CD=45°.
故选B.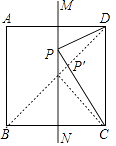
【考点精析】解答此题的关键在于理解正方形的性质的相关知识,掌握正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形,以及对轴对称-最短路线问题的理解,了解已知起点结点,求最短路径;与确定起点相反,已知终点结点,求最短路径;已知起点和终点,求两结点之间的最短路径;求图中所有最短路径.


 智慧小复习系列答案
智慧小复习系列答案科目:初中数学 来源: 题型:
【题目】(1)如图1:在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°.E,F分别是BC,CD上的点.且∠EAF=60°.探究图中线段BE,EF,FD之间的数量关系.
小王同学探究此问题的方法是,延长FD到点G.使DG=BE.连结AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是 ;
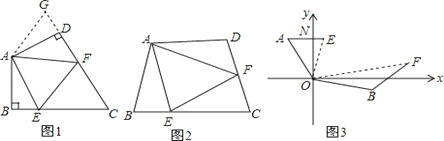
(2)如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°.E,F分别是BC,CD上的点,且∠EAF=![]() ∠BAD上述结论是否仍然成立,并说明理由;
∠BAD上述结论是否仍然成立,并说明理由;
(3)如图3,在某次军事演习中,舰艇甲在指挥中心(O处)北偏西30°的A处,舰艇乙在指挥中心南偏东70°的B处,并且两舰艇到指挥中心的距离相等,接到行动指令后,舰艇甲向正东方向以60海里/小时的速度前进,舰艇乙沿北偏东50°的方向以80海里/小时的速度前进1.5小时后,指挥中心观测到甲、乙两舰艇分别到达E,F处,且两舰艇之间的夹角为70°,试求此时两舰艇之间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
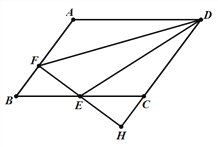
【题目】如图,在□ABCD中,AB=3,AD=4,∠ABC=60°,过BC的中点E作EF⊥AB于F,与DC的延长线相交于点H.
(1)求证:△BEF≌△CEH;
(2)求DE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com