
【题目】如图,已知点A(a,b),B(1,6)为平面直角坐标系内两点,且a,b满足b=![]() ﹣
﹣![]() +2,AB的延长线交y轴于点C.
+2,AB的延长线交y轴于点C.

(1)点A的坐标为 (直接写出结果);
(2)如图1,点P(m,4)为线段AB上的点.
①点C坐标为 (直接写出结果)
②求m的值;
(3)如图2,若Q为第四象限直线AB上一点,将QC绕Q点逆时针旋转50°,交x轴负半轴于点D,在第二象限内有点E,使x轴、y轴分别平分∠EDQ,∠ECQ,试求∠CED的度数,
【答案】(1)(3,2);(2)①(0,8);②2;(3)130°.
【解析】
(1)利用二次根式的性质求出a,b的值即可解决问题.
(2)①求出AB解析式即可解决问题.
②由S△AEC=S△PCF+S四边形AEFP,可得![]() AEEC=
AEEC=![]() CFPF+
CFPF+![]() (AE+PF)EF,由此构建方程解决问题即可.
(AE+PF)EF,由此构建方程解决问题即可.
(3)如图2中,分别过C,E,Q作直线l∥x轴,EF∥x轴,QG∥x轴.由题意设∠EDO=∠QDO=x.则∠DQG=∠ODQ=x,利用平行线的性质解决问题即可.
解:(1)∵b=![]() ﹣
﹣![]() +2,
+2,
又∵![]() ,
,
∴a=3,b=2,
∴A(3,2),
故答案为(3,2).
(2)①设AB的解析式为y=kx+b(k≠0)
把A(3,2),B(1,6)代入得![]()
解得![]()
∴AB的解析式为y=-2x+8
令x=0,解得y=8
∴C(0,8).
故答案为(0,8).
②如图1中,作AE⊥OC于E,OF⊥OC于F.
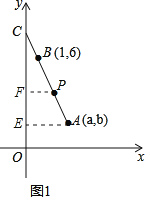
∵S△AEC=S△PCF+S四边形AEFP,
∴![]() AEEC=
AEEC=![]() CFPF+
CFPF+![]() (AE+PF)EF,
(AE+PF)EF,
∵A(3,2),B(1,6),C(0,8),P(m,4),
∴![]() ×3×6=
×3×6=![]() ×4×m+
×4×m+![]() ×2×(m+3),
×2×(m+3),
解答m=2.
(3)如图2中,分别过C,E,Q作直线l∥x轴,EF∥x轴,QG∥x轴.
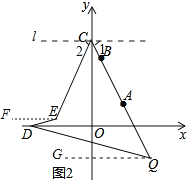
由题意设∠EDO=∠QDO=x.则∠DQG=∠ODQ=x,
∵直线l∥EF∥GQ,
∴∠1=∠2=∠CQG=50°+x,∠FEC=180°﹣∠2=130°﹣x,
∵∠FED=∠EDO=x,
∴∠CED=∠FEC+∠FED=130°﹣x+x=130°.


 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:初中数学 来源: 题型:
【题目】某网店销售某款童装,每件售价60元,每星期可卖300件,为了促销,该网店决定降价销售.市场调查反映:每降价1元,每星期可多卖30件.已知该款童装每件成本价40元,设该款童装每件售价x元,每星期的销售量为y件.
(1)求y与x之间的函数关系式;
(2)当每件售价定为多少元时,每星期的销售利润最大,最大利润多少元?
(3)若该网店每星期想要获得不低于6480元的利润,每星期至少要销售该款童装多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某区举行“庆祝改革开放40周年”征文比赛,已知每篇参赛征文成绩记![]() 分
分![]() ,组委会从1000篇征文中随机抽取了部分参赛征文,统计了他们的成绩,并绘制了如下不完整的两幅统计图表:
,组委会从1000篇征文中随机抽取了部分参赛征文,统计了他们的成绩,并绘制了如下不完整的两幅统计图表:
征文比赛成绩频数分布表 | ||
分数段 | 频数 | 频率 |
| 38 | 0.38 |
| 0.32 | |
| ||
| 10 | 0.1 |
合计 | 1 | |

请根据以上信息,解决下列问题:
(1)征文比赛成绩频数分布表中![]() 的值是 ;
的值是 ;
(2)补全征文比赛成绩频数分布直方图;
(3)若80分以上(含80分)的征文将被评为一等奖,试估计全市获得一等奖征文的篇数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD由四个相同的大长方形,四个相同的小长形以及一个小正方形组成,其中四个大长方形的长和宽分别是小长方形长和宽的2倍,若中间小正方形的面积为1,则大正方形ABCD的面积是( )
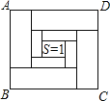
A.36B.25C.20D.16
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两个学校乐团,决定向某服装厂购买同样的演出服。下面是服装厂给出的演出服装的价格表:经调查:两个乐团共75人(甲乐团人数不少于40人),如果分别各自购买演出服,按每人一套的标准两个乐团共需花费5600元。请回答以下问题:
购买服装的套数 | 1~39套(含39套) | 40~79套(含79套) | 80套及以上 |
每套服装的价格 | 80元 | 70元 | 60元 |
(1)如果甲、乙两个乐团联合起来购买服装,那么比各自购买服装最多可以节省多少元?
(2)甲、乙两个乐团各有多少人?
(3)现从甲乐团抽调a人,从乙乐团抽调b人(要求从每个乐团抽调的人数不少于5人),去儿童福利院献爱心演出,并在演出后每位乐团成员向儿童们进行“心连心活动”;甲乐团每位成员负责3位小朋友,乙乐团每位成员负责5位小朋友,这样恰好使得福利院65位小朋友全部得到“心连心活动”的温暖。请写出所有的抽调方案,并说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】出租车司机小李某天上午营运时是在东西走向的大街上进行的,如果规定向东为正,向西为负,他这天上午所接六位乘客的行车里程(单位:![]() )如下:
)如下:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
问:(1)将最后一位乘客送到目的地时,小李在什么位置?
(2)若汽车耗油量为![]() (升/千米),这天上午小李接送乘客,出租车共耗油多少升?
(升/千米),这天上午小李接送乘客,出租车共耗油多少升?
(3)若出租车起步价为8元,起步里程为![]() (包括
(包括![]() ),超过部分每千米1.2元,问小李这天上午共得车费多少元?
),超过部分每千米1.2元,问小李这天上午共得车费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O是坐标原点,过点A(﹣1,0)的抛物线y=x2﹣bx﹣3与x轴的另一个交点为B,与y轴交于点C,其顶点为D点.
(1)求b的值以及点D的坐标;
(2)连接BC、BD、CD,在x轴上是否存在点P,使得以A、C、P为顶点的三角形与△BCD相似.若存在,求出点P的坐标;若不存在,说明理由;
(3)动点Q的坐标为(m,1).
①当△BCQ是以BC为直角边的直角三角形时,求m的值;
②连接OQ、CQ,求△CQO的外接圆半径的最小值,并求出此时点Q的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小张骑自行车匀速从甲地到乙地,在途中休息了-段时间后,仍按原速行驶他距乙地的距离与时间的关系如图中折线所示,小李骑摩托车匀速从乙地到甲地,比小张晚出发一段时间,他距乙地的距离与时间的关系如图中线段AB所示,
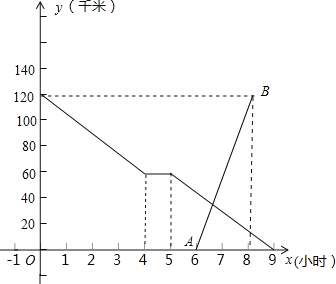
(1)小李到达甲地后,再经过 小时小张到达乙地;小张骑自行车的速度是 千米/小时;
(2)请你写出小李距乙地的距离y(千米)与时间x(小时)之间的函数关系(不要求写出定义域);
(3)若小李想在小张休息期间(第4小时和第5小时不算小张休息)与他相遇,则他出发的时间x应在什么范围?(直接写出答案)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com