
分析 (1)原式利用多项式除以单项式法则计算即可得到结果;
(2)原式利用幂的乘方与积的乘方运算法则计算,合并即可得到结果;
(3)原式利用零指数幂法则,积的乘方运算法则计算即可得到结果;
(4)原式第一项利用乘方的意义计算,第二项利用零指数幂法则计算,第三项利用乘方的意义计算,最后一项利用负整数指数幂法则计算即可得到结果;
(5)原式利用完全平方公式及平方差公式化简即可得到结果;
(6)原式利用多项式除以单项式,以及单项式乘以多项式法则计算即可得到结果.
解答 解:(1)原式=2x2-3xy+6y2;
(2)原式=a6+4a6-a6=4a6;
(3)原式=1+(-0.125×8)2014×8=9;
(4)原式=-1-1+8-16=-10;
(5)原式=x2+4+4x-2x2+8+x2+4-4x=16;
(6)原式=-2a2+4a-3-a-2a2=-4a2+3a-3.
点评 此题考查了整式的混合运算,熟练掌握运算法则是解本题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
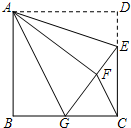 如图,正方形ABCD中,CD=6,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连结AG、CF.
如图,正方形ABCD中,CD=6,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连结AG、CF.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com