
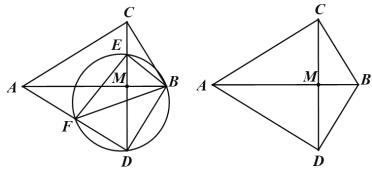
【题目】如图,在△ABC中,∠ACB=90°,将△ABC沿直线AB翻折得到△ABD,连接CD交AB于点M.E是线段CM上的点,连接BE.F是△BDE的外接圆与AD的另一个交点,连接EF,BF,
(1)求证:△BEF是直角三角形;
(2)求证:△BEF∽△BCA;
(3)当AB=6,BC=m时,在线段CM正存在点E,使得EF和AB互相平分,求m的值.
【答案】(1)见解析;(2)见解析;(3)![]()
【解析】
(1)想办法证明∠BEF=90°即可解决问题(也可以利用圆内接四边形的性质直接证明).
(2)根据两角对应相等两三角形相似证明.
(3)证明四边形AFBE是平行四边形,推出FJ=![]() BD=
BD=![]() m,EF=m,由△ABC∽△CBM,可得BM=
m,EF=m,由△ABC∽△CBM,可得BM=![]() ,由△BEF∽△BCA,推出
,由△BEF∽△BCA,推出![]() ,由此构建方程求解即可.
,由此构建方程求解即可.
(1)证明:由折叠可知,∠ADB=∠ACB=90°
∵∠EFB=∠EDB,∠EBF=∠EDF,
∴∠EFB+∠EBF=∠EDB+∠EDF=∠ADB=90°,
∴∠BEF=90°,
∴△BEF是直角三角形.
(2) 证明:∵BC=BD,
∴∠BDC=∠BCD,
∵∠EFB=∠EDB,
∴∠EFB=∠BCD,
∵AC=AD,BC=BD,
∴AB⊥CD,
∴∠AMC=90°,
∵∠BCD+∠ACD=∠ACD+∠CAB=90°,
∴∠BCD=∠CAB,
∴∠BFE=∠CAB,
∵∠ACB=∠FEB=90°,
∴△BEF∽△BCA.
(3) 设EF交AB于J.连接AE,如下图所示:
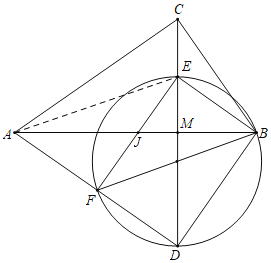
∵EF与AB互相平分,
∴四边形AFBE是平行四边形,
∴∠EFA=∠FEB=90°,即EF⊥AD,
∵BD⊥AD,
∴EF∥BD,
∵AJ=JB,
∴AF=DF,
∴ FJ=![]()
∴ EF=![]()
∵ △ABC∽△CBM
∴ BC:MB=AB:BC
∴ BM=![]() ,
,
∵ △BEJ∽△BME,
∴ BE:BM=BJ:BE
∴ BE=![]() ,
,
∵ △BEF∽△BCA,
∴![]()
即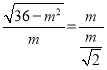
解得![]() (负根舍去).
(负根舍去).
故答案为:![]()


 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案科目:初中数学 来源: 题型:
【题目】如图,已知:AB是⊙O的直径,点C在⊙O上,CD是⊙O的切线,AD⊥CD于点D.E是AB延长线上一点,CE交⊙O于点F,连结OC,AC.

(1)求证:AC平分∠DAO;
(2)若∠DAO=105°,∠E=30°.①求∠OCE的度数.②若⊙O的半径为![]() ,求线段EF的长.
,求线段EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】黔东南州某超市购进甲、乙两种商品,已知购进3件甲商品和2件乙商品,需60元;购进2件甲商品和3件乙商品,需65元.
(1)甲、乙两种商品的进货单价分别是多少?
(2)设甲商品的销售单价为x(单位:元/件),在销售过程中发现:当11≤x≤19时,甲商品的日销售量y(单位:件)与销售单价x之间存在一次函数关系,x、y之间的部分数值对应关系如表:
销售单价x(元/件) | 11 | 19 |
日销售量y(件) | 18 | 2 |
请写出当11≤x≤19时,y与x之间的函数关系式.
(3)在(2)的条件下,设甲商品的日销售利润为w元,当甲商品的销售单价x(元/件)定为多少时,日销售利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在正方形![]() 中,对角线
中,对角线![]() 相交于点
相交于点![]() ,点
,点![]() 为线段
为线段![]() 上一点,连接
上一点,连接![]() ,将
,将![]() 绕
绕![]() 点顺时针旋转
点顺时针旋转![]() 得到
得到![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() .
.
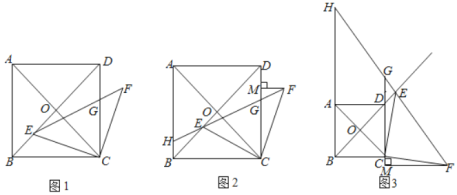
(1)若![]() ,求
,求![]() 的面积;
的面积;
(2)如图2,线段![]() 的延长线交
的延长线交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,求证:
,求证:![]() ;
;
(3)如图3,点![]() 为射线
为射线![]() 上一点,线段
上一点,线段![]() 的延长线交直线
的延长线交直线![]() 于点
于点![]() ,交直线
,交直线![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 垂直直线
垂直直线![]() 于点
于点![]() ,请直接写出线段
,请直接写出线段![]() 的数量关系.
的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
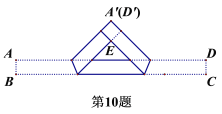
【题目】把一张宽为1cm的长方形纸片ABCD折叠成如图所示的阴影图案,顶点A,D互相重合,中间空白部分是以E为直角顶点,腰长为2cm的等腰直角三角形,则纸片的长AD(单位:cm)为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,AB为
中,AB为![]() 的直径,C为
的直径,C为![]() 上一点,P是
上一点,P是![]() 的中点,过点P作AC的垂线,交AC的延长线于点D.
的中点,过点P作AC的垂线,交AC的延长线于点D.
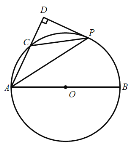
(1)求证:DP是![]() 的切线;
的切线;
(2)若AC=5,![]() ,求AP的长.
,求AP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
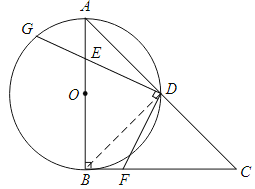
【题目】如图,在RtΔABC中,∠ABC=90°,AB=CB,以AB为直径的⊙O交AC于点D,点E是AB边上一点(点E不与点A、B重合),DE的延长线交⊙O于点G,DF⊥DG,且交BC于点F.
(1)求证:AE=BF;
(2)连接EF,求证:∠FEB=∠GDA;
(3)连接GF,若AE=2,EB=4,求ΔGFD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一个矩形纸片![]() ,将该纸片放置在平面直角坐标系中,点
,将该纸片放置在平面直角坐标系中,点![]() ,点
,点![]() ,点P为
,点P为![]() 边上的动点.
边上的动点.
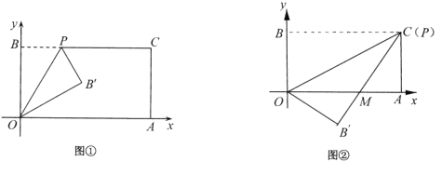
(1)如图①,经过点O、P折叠该纸片,得点![]() 和折痕
和折痕![]() .当点P的坐标为
.当点P的坐标为![]() 时,求
时,求![]() 的度数;
的度数;
(2)如图②,当点P与点C重合时,经过点O、P折叠纸片,使点B落在点![]() 的位置,
的位置,![]() 与
与![]() 交于点M,求点M的坐标;
交于点M,求点M的坐标;
(3)过点P作直线![]() ,交
,交![]() 于点Q,再取
于点Q,再取![]() 中点T,
中点T,![]() 中点N,分别以
中点N,分别以![]() ,
,![]() ,
,![]() ,
,![]() 为折痕,依次折叠该纸片,折叠后点O的对应点与点B的对应点恰好重合,且落在线段
为折痕,依次折叠该纸片,折叠后点O的对应点与点B的对应点恰好重合,且落在线段![]() 上,A、C的对应点也恰好重合,也落在线段
上,A、C的对应点也恰好重合,也落在线段![]() 上,求此时点P的坐标(直接写出结果即可).
上,求此时点P的坐标(直接写出结果即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装公司有![]() 型童装80件,
型童装80件,![]() 型童装120件,分配给下属的“万达”和“万象城”两个专卖店销售,其中140件给万达店,60件给万象城店,且都能卖完,两商店销售这两种童装每件的利润(元)如表:
型童装120件,分配给下属的“万达”和“万象城”两个专卖店销售,其中140件给万达店,60件给万象城店,且都能卖完,两商店销售这两种童装每件的利润(元)如表:
|
| |
万达店 | 100 | 80 |
万象城店 | 80 | 90 |
(1)设分配给万达店![]() 型产品
型产品![]() 件(
件(![]() ),请在下表中用含
),请在下表中用含![]() 的代数式填写:
的代数式填写:
|
| |
万达店 |
| ______ |
万象城店 | ______ | ______ |
若记这家服装公司卖出这200件产品的总利润为![]() (元),求
(元),求![]() 关于
关于![]() 的函数关系.
的函数关系.
(2)现要求总利润不低于18140元,请说明有多少种不同分配方案,并写出各种分配方案.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com