
【题目】我们给出如下定义:若一个四边形中存在相邻两边的平方和等于一条对角线的平方,则称这个四边形为勾股四边形,这两条相邻的边称为这个四边形的勾股边.

(1)写出你所学过的特殊四边形中是勾股四边形的两种图形的名称 , ;
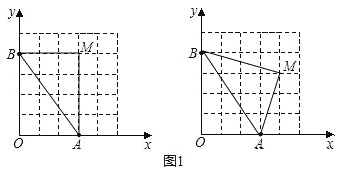
(2)如图1,已知格点(小正方形的顶点)O(0,0),A(3,0),B(0,4),请你直接写出所有以格点为顶点,OA、OB为勾股边且有对角线相等的勾股四边形OAMB的顶点M的坐标.
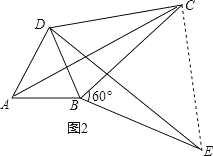
(3)如图2,将△ABC绕顶点B按顺时针方向旋转60°,得到ADBE,连接AD、DC,∠DCB=30°.求证:DC+BC=AC,即四边形ABCD是勾股四边形.
(4)如图,将△ABC绕顶点B按顺时针方向旋转(0°<a<90°),得到ADBE,连接AD、DC,则∠DCB= °,四边形ABCD是勾股四边形.
【答案】(1)矩形,正方形;(2)M(3,4),M(4,3);(3)证明见解析;(4)![]() .
.
【解析】
试题分析:(1)根据定义和勾股四边形的性质,有矩形或正方形或直角梯形满足题意;
(2)OM=AB知以格点为顶点的M共两个,分别得出答案;
(3)连接CE,证明△BCE是等边三角形,△DCE是直角三角形,继而可证明四边形ABCD是勾股四边形;
(4)连接CE,证明△DCE是直角三角形,继而可证明四边形ABCD是勾股四边形.
试题解析:(1)学过的特殊四边形中是勾股四边形的两种图形的名称:矩形,正方形;
(2)如图1所示:M(3,4),M(4,3);
(3)如图2,连接CE,由旋转得:△ABC≌△DBE,
∴AC=DE,BC=BE,
∵∠CBE=60,
∴△CBE为等边三角形,
∴BC=CE,∠BCE=60,
∵∠DCB=30,
∴∠DCE=∠DCB+∠BCE=30°+60°=90°,
∴DC2+EC2=DE2,
∴DC2+BC2=AC2.
∴即四边形ABCD是勾股四边形.
(4)如图3,当∠DCB=![]() ,四边形ABCD是勾股四边形,
,四边形ABCD是勾股四边形,
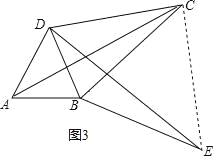
理由:连接CE,
由旋转得:△ABC≌△DBE,
∴AC=DE,BC=BE,
又∵∠CBE=α,
∴∠BCE=∠BEC=90°-![]() ,
,
∴∠DCE=90°,
∴DC2+EC2=DE2,
∴DC2+BC2=AC2.
∴即四边形ABCD是勾股四边形


 每课必练系列答案
每课必练系列答案科目:初中数学 来源: 题型:
【题目】△ABC与△A′B′C′在平面直角坐标系中的位置如图.
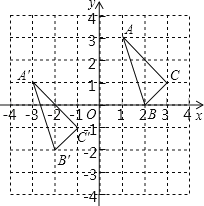
(1)分别写出下列各点的坐标:A′ ; B′ ;C′ ;
(2)说明△A′B′C′由△ABC经过怎样的平移得到? .
(3)若点P(a,b)是△ABC内部一点,则平移后△A′B′C′内的对应点P′的坐标为 ;
(4)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国计划在2020年左右发射火星探测卫星,据科学研究测量,火星距离地球的最近距离约为5500万千米,这个数据用科学计数法表示为
A. 5.5×106 B. 5.5×107 C. 55×107 D. 0.55×108
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com