阅读下面材料：
在数学课上，老师提出如下问题：
|
小芸的作法如下：
|
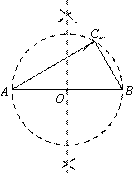
老师说：“小芸的作法正确．”
请回答：小芸的作法中判断∠ACB是直角的依据是 ．
开心快乐假期作业暑假作业西安出版社系列答案
名题训练系列答案
期末集结号系列答案科目：初中数学 来源： 题型：
我们知道，三角形的三条中线一定会交于一点，这一点就叫做三角形的重心。重心有很多美妙的性质，如有关线段比．面积比就有一些“漂亮”结论，利用这些性质可以解决三角形中的若干问题。
请你利用重心的概念完成如下问题：
 |
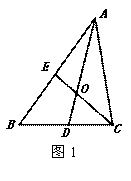
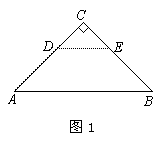
（1）如图1，△ABC的中线AD、CE的交点O为三角形的重心，利用三角形的中位线可以证明：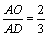
，请你完成该证明；
（2）运用第（1）的结论解决以下问题：
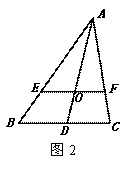
①小丽说：“过三角形的重心任画一条直线都能将三角形的面积平分”。小
明想了想说：“这个说法是错误的。”他过点O画出了BC的平行线，交AB、AC于点E、F，如图2，你能求出
的值吗？谁的说法正确？
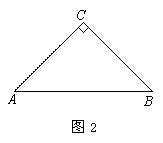
②△ABC中，∠C＝90°，AB=6cm，求△ABC的重心与外心的距离。
查看答案和解析>>
科目：初中数学 来源： 题型：
如图，在边长为1的小正方形组成的网格中，△ABC的三个顶点均在格点上．将△ABC绕点A顺时针旋转90°得到△AB1C1．
(1) 在网格中画出△AB1C1；
(2) 计算点B旋转到B1的过程中所经过的路径长．（结果保留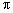
）
 |
查看答案和解析>>
科目：初中数学 来源： 题型：
如图1，△ABC和△CDE都是等腰直角三角形，∠C＝90°，将△CDE绕点C逆时针旋转一个角度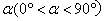
，使点A，D，E在同一直线上，连接AD，BE．
(1) ① 依题意补全图2；
② 求证：AD＝BE，且AD⊥BE；
③ 作CM⊥DE，垂足为M，请用等式表示出线段CM，AE，BE之间的数量关系；
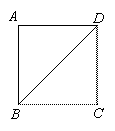(2) 如图3，正方形ABCD边长为
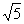，若点P满足PD＝1，且∠BPD＝90°，请直接写出点A到BP的距离．
 |  | ||||
| |||||
查看答案和解析>>
科目：初中数学 来源： 题型：
某校七年级共有589名学生分别到北京博物馆和中国科技馆学参观，其中到北京博物馆的人数比到中国科技馆人数的2倍还多56人．设到中国科技馆的人数为x人，可列方程为 ．
查看答案和解析>>
科目：初中数学 来源： 题型：
．阅读下面材料：
一个含有多个字母的式子中，如果任意交换两个字母的位置，式子的值都不变，这样的式子就叫做对称式. 例如：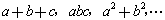
含有两个字母a，b的对称式的基本对称式是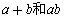
，像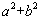
，
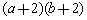等对称式都可以用
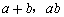表示，例如：
.
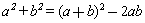请根据以上材料解决下列问题：
（1）式子①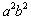 
②
③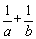
中，属于对称式的是_________(填序号)；
（2）已知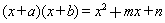
.
①若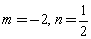
，求对称式
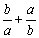的值；
②若
，直接写出对称式
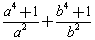的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
