练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】植树节期间，某单位欲购进A、B两种树苗，若购进A种树苗3棵，B种树苗5颗，需2100元，若购进A种树苗4颗，B种树苗10颗，需3800元．
    （1）求购进A、B两种树苗的单价；
    （2）若该单位准备用不多于8000元的钱购进这两种树苗共30棵，求A种树苗至少需购进多少棵？

    【答案】
    （1）解：设B树苗的单价为x元，则A树苗的单价为y元，可得： ，

    解得： ，

    答：B树苗的单价为300元，A树苗的单价为200元


    （2）解：设购买A种树苗a棵，则B种树苗为（30﹣a）棵，

    可得：200a+300（30﹣a）≤8000，

    解得：a≥10，

    答：A种树苗至少需购进10棵


    【解析】（1）设B树苗的单价为x元，则A树苗的单价为y元．则由等量关系列出方程组解答即可；（2）设购买A种树苗a棵，则B种树苗为（30﹣a）棵，然后根据总费用和两种树的棵数关系列出不等式解答即可．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】一辆客车从甲地出发前往乙地，平均速度v（千米/小时）与所用时间t（小时）的函数关系如图所示，其中60≤v≤120．
    （1）直接写出v与t的函数关系式；
    （2）若一辆货车同时从乙地出发前往甲地，客车比货车平均每小时多行驶20千米，3小时后两车相遇．
    ①求两车的平均速度；
    ②甲、乙两地间有两个加油站A、B，它们相距200千米，当客车进入B加油站时，货车恰好进入A加油站（两车加油的时间忽略不计），求甲地与B加油站的距离．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，把正方形铁片OABC置于平面直角坐标系中，顶点A的坐标为（3，0），点P（1，2）在正方形铁片上，将正方形铁片绕其右下角的顶点按顺时针方向依次旋转90°，第一次旋转至图①位置，第二次旋转至图②位置…，则正方形铁片连续旋转2017次后，点P的坐标为 ．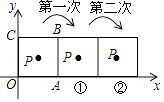

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】我们定义：如图1，在△ABC看，把AB点绕点A顺时针旋转α（0°＜α＜180°）得到AB'，把AC绕点A逆时针旋转β得到AC'，连接B'C'．当α+β=180°时，我们称△A'B'C'是△ABC的“旋补三角形”，△AB'C'边B'C'上的中线AD叫做△ABC的“旋补中线”，点A叫做“旋补中心”．

    （1）在图2，图3中，△AB'C'是△ABC的“旋补三角形”，AD是△ABC的“旋补中线”．①如图2，当△ABC为等边三角形时，AD与BC的数量关系为AD=BC；
    ②如图3，当∠BAC=90°，BC=8时，则AD长为 ．
    （2）在图1中，当△ABC为任意三角形时，猜想AD与BC的数量关系，并给予证明．
    （3）如图4，在四边形ABCD，∠C=90°，∠D=150°，BC=12，CD=2 ，DA=6．在四边形内部是否存在点P，使△PDC是△PAB的“旋补三角形”？若存在，给予证明，并求△PAB的“旋补中线”长；若不存在，说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】计算题
    （1）计算：|﹣3|+（ +π）0﹣（﹣ ）﹣2﹣2cos60°；
    （2）先化简，在求值：（ ﹣ ）+ ，其中a=﹣2+ ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在三角形纸片ABC中，∠A=90°，∠C=30°，AC=30cm，将该纸片沿过点B的直线折叠，使点A落在斜边BC上的一点E处，折痕记为BD（如图1），减去△CDE后得到双层△BDE（如图2），再沿着过△BDE某顶点的直线将双层三角形剪开，使得展开后的平面图形中有一个是平行四边形，则所得平行四边形的周长为cm．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】甲、乙、丙三位运动员在相同条件下各射靶10次，每次射靶的成绩如下：
    甲：9，10，8，5，7，8，10，8，8，7
    乙：5，7，8，7，8，9，7，9，10，10
    丙：7，6，8，5，4，7，6，3，9，5
    （1）根据以上数据完成下表：

    平均数

    中位数

    方差

    甲

    8

    8

    乙

    8

    8

    2.2

    丙

    6

    3


    （2）根据表中数据分析，哪位运动员的成绩最稳定，并简要说明理由；
    （3）比赛时三人依次出场，顺序由抽签方式决定，求甲、乙相邻出场的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，已知CA=CB=5，BA=6，点E是线段AB上的动点（不与端点重合），点F是线段AC上的动点，连接CE、EF，若在点E、点F的运动过程中，始终保证∠CEF=∠B．
    （1）求证：∠AEF=∠BCE；
    （2）当以点C为圆心，以CF为半径的圆与AB相切时，求BE的长；
    （3）探究：在点E、F的运动过程中，△CEF可能为等腰三角形吗？若能，求出BE的长；若不能，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，方格纸中的每个小方格都是边长为1的正方形，我们把以格点间连线为边的三角形称为“格点三角形”，图中的△ABC就是格点三角形，建立如图所示的平面直角坐标系，点C的坐标为（0，﹣1）．

    （1）在如图的方格纸中把△ABC以点O为位似中心扩大，使放大前后的位似比为1：2，画出△A1B2C2（△ABC与△A1B2C2在位似中心O点的两侧，A，B，C的对应点分别是A1 ， B2 ， C2）．
    （2）利用方格纸标出△A1B2C2外接圆的圆心P，P点坐标是 ， ⊙P的半径= ． （保留根号）

    查看答案和解析>>

    同步练习册答案