
【题目】在平面直角坐标系![]() 中的点
中的点![]()
![]() ,将它的纵坐标
,将它的纵坐标![]() 与横坐标
与横坐标![]() 的比称为点
的比称为点![]() 的“湘一比”,记为
的“湘一比”,记为![]() ,如点
,如点![]() ,则
,则![]() .
.
(1)若![]() 在直线
在直线![]() 上,求点
上,求点![]() 的“湘一比”
的“湘一比”![]() 及直线
及直线![]() 与
与![]() 轴夹角的正切值;
轴夹角的正切值;
(2)已知点![]() 的“湘一比”
的“湘一比”![]() 为
为![]() ,且
,且![]() 在
在![]() 上,
上,![]() 的半径为
的半径为![]() ,若点
,若点![]() 在
在![]() 上,求
上,求![]() 的“湘一比”
的“湘一比”![]() 的取值范围;
的取值范围;
(3)设![]() 、
、![]() 为正整数,且
为正整数,且![]() ,对一切实数
,对一切实数![]() ,如果直线
,如果直线![]() 与二次函数
与二次函数![]() 交于
交于![]() 、
、![]() ,且
,且![]() ,求点
,求点![]() 的“湘一比”
的“湘一比”![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 或
或![]()
【解析】
(1)根据“湘一比”的定义求出a的值,即可得出结论;
(2)先确定出点Q的坐标,进而判断出直线OM和⊙Q相切时,两种情况即可得出kM的最大值和最小值,就是分界点,即可得出结论;
(3)先求出x1=-3,x2=mt,进而建立不等式组 ,得出m>2且(mn-6)2≤0,即可得出结论.
,得出m>2且(mn-6)2≤0,即可得出结论.
解:(1) ![]() 在直线
在直线![]() 上,
上,
![]() ,
,
![]() ,
,
![]() ,此时直线
,此时直线![]() 与
与![]() 轴夹角的正切值为
轴夹角的正切值为![]() ;
;
(2)由题意知,![]()
![]() ,
,
 ,
,
![]() 在
在![]() 上,
上,
![]()
![]() 或
或![]() (舍),
(舍),
![]()
根据点![]() 的”纵横比”知,直线
的”纵横比”知,直线![]() 和
和![]() 相切时,一个是
相切时,一个是![]() 的最大值和另一个是最小值,
的最大值和另一个是最小值,
当![]() 时,
时, ![]() 最小, 此时
最小, 此时![]() ,
,
当 时,
时,![]() 最大,此时
最大,此时![]() ,
,
![]()
(3)由题意知,![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
∵等于一切实数![]() 不等式恒成立,
不等式恒成立,
 ,
,
![]() 为正整数,
为正整数,
![]() 且
且![]()
![]() ,
,
![]() ,
,
![]() 为正整数,
为正整数,
![]() 或
或![]() ,
,![]() ,
,
![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】一名在校大学生利用“互联网+”自主创业,销售一种产品,这种产品的成本价10元/件,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于16元/件,市场调查发现,该产品每天的销售量![]() (件
(件![]() 与销售价
与销售价![]() (元/件)之间的函数关系如图所示.
(元/件)之间的函数关系如图所示.
(1)求![]() 与
与![]() 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
(2)求每天的销售利润W(元![]() 与销售价
与销售价![]() (元/件)之间的函数关系式,并求出每件销售价为多少元时,每天的销售利润最大?最大利润是多少?
(元/件)之间的函数关系式,并求出每件销售价为多少元时,每天的销售利润最大?最大利润是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
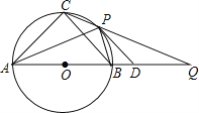
【题目】如图,⊙O为等腰三角形ABC的外接圆,AB是⊙O的直径,AB=12,P为![]() 上任意一点(不与点B,C重合),直线CP交AB的延长线于点Q,⊙O在点P处的切线PD交BQ于点D,则下列结论:①若∠PAB=30°,则
上任意一点(不与点B,C重合),直线CP交AB的延长线于点Q,⊙O在点P处的切线PD交BQ于点D,则下列结论:①若∠PAB=30°,则![]() 的长为π;②若PD∥BC,则AP平分∠CAB;③若PB=BD,则PD=6
的长为π;②若PD∥BC,则AP平分∠CAB;③若PB=BD,则PD=6![]() ;④无论点P在
;④无论点P在![]() 上的位置如何变化,CPCQ=108.其中正确结论的序号为 ______.
上的位置如何变化,CPCQ=108.其中正确结论的序号为 ______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了落实党的“精准扶贫”政策,A、B两城决定向C、D两乡运送肥料以支持农村生产,已知A、B两城共有肥料500吨,其中A城肥料比B城少100吨,从A城往C、D两乡运肥料的费用分别为20元/吨和25元/吨;从B城往C、D两乡运肥料的费用分别为15元/吨和24元/吨.现C乡需要肥料240吨,D乡需要肥料260吨.
(1)A城和B城各有多少吨肥料?
(2)设从A城运往C乡肥料x吨,总运费为y元,求出最少总运费.
(3)由于更换车型,使A城运往C乡的运费每吨减少a(0<a<6)元,这时怎样调运才能使总运费最少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如表
x | ﹣1 | 0 | 1 | 3 |
y | ﹣1 | 3 | 5 | 3 |
下列结论:
①ac<0;
②当x>1时,y的值随x值的增大而减小.
③3是方程ax2+(b﹣1)x+c=0的一个根;
④当﹣1<x<3时,ax2+(b﹣1)x+c>0.
其中正确的结论是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】规定:[x]表示不大于x的最大整数,(x)表示不小于x的最小整数,[x)表示最接近x的整数(x≠n+0.5,n为整数),例如:[2.3]=2,(2.3)=3,[2.3)=2.则下列说法正确的是________.(写出所有正确说法的序号)
①当x=1.7时,[x]+(x)+[x)=6;
②当x=﹣2.1时,[x]+(x)+[x)=﹣7;
③方程4[x]+3(x)+[x)=11的解为1<x<1.5;
④当﹣1<x<1时,函数y=[x]+(x)+x的图象与正比例函数y=4x的图象有两个交点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国中东部地区雾霾天气趋于严重,环境治理已刻不容缓.我市某电器商场根据民众健康需要,代理销售某种家用空气净化器,其进价是200元/台.经过市场销售后发现:在一个月内,当售价是400元/台时,可售出200台,且售价每降低10元,就可多售出50台.若供货商规定这种空气净化器售价不能低于300元/台,代理销售商每月要完成不低于450台的销售任务.
(1)试确定月销售量y(台)与售价x(元/台)之间的函数关系式;并求出自变量x的取值范围;
(2)当售价x(元/台)定为多少时,商场每月销售这种空气净化器所获得的利润w(元)最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为4,点O为对角线AC、BD的交点,点E为边AB的中点,△BED绕着点B旋转至△BD1E1,如果点D、E、D1在同一直线上,那么EE1的长为______.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com