
【题目】如图,在正方形ABCD的对角线AC上取点E,使得∠CDE=15°,连接BE.延长BE到F,连接CF,使得CF=BC.
(1)求证:DE=BE;
(2)求证:EF=CE+DE.

【答案】(1)证明见解析;(2)证明见解析.
【解析】试题分析:(1)由正方形的性质可以得出AB=AD,∠BAC=∠DAC=45°,通过证明△ABE≌△ADE,就可以得出结论;
(2)在EF上取一点G,使EG=EC,连结CG,再通过条件证明△DEC≌△FGC就可以得出结论.
试题解析:(1)∵四边形ABCD是正方形,
∴AB=AD,∠ABC=∠ADC=90°,
∠BAC=∠DAC=45°.
∵在△ABE和△ADE中,  ,
,
∴△ABE≌△ADE(SAS),
∴BE=DE.
(2)在EF上取一点G,使EG=EC,连结CG,

∵△ABE≌△ADE,
∴∠ABE=∠ADE.
∴∠CBE=∠CDE,
∵BC=CF,∴∠CBE=∠F,
∵∠CDE=15°,∴∠CBE=15°,
∴∠CEG=60°.
∵CE=GE,∴△CEG是等边三角形.
∴∠CGE=60°,CE=GC,
∴∠GCF=45°,
∴∠ECD=GCF.
∵在△DEC和△FGC中,  ,
,
∴△DEC≌△FGC(SAS),
∴DE=GF.
∵EF=EG+GF,
∴EF=CE+ED.


 精英口算卡系列答案
精英口算卡系列答案科目:初中数学 来源: 题型:
【题目】我们规定:若![]() =(a,b),
=(a,b),![]() =(c,d),则
=(c,d),则![]() ·
·![]() =ac+bd.如
=ac+bd.如
![]() =(1,2),
=(1,2),![]() =(3,5),则
=(3,5),则![]() ·
·![]() =1×3+2×5=13.
=1×3+2×5=13.
(1)已知![]() =(2,4),
=(2,4),![]() =(2,-3),求
=(2,-3),求![]() ·
·![]() ;
;
(2)已知![]() =(x-1,1),
=(x-1,1),![]() =(x-1,x+1),求y=
=(x-1,x+1),求y=![]() ·
·![]() ;
;
(3)判断y=![]() ·
·![]() 的函数图象与一次函数y=x-1的图象是否相交,请说明理由.
的函数图象与一次函数y=x-1的图象是否相交,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点E在直角△ABC的斜边AB上,以AE为直径的⊙O与直角边BC相切于点D.
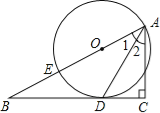
(1)求证:AD平分∠BAC;
(2)若BE=2,BD=4,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】张老师计划到超市购买甲种文具100个,他到超市后发现还有乙种文具可供选择.如果调整文具的购买品种,每减少购买1个甲种文具,需增加购买2个乙种文具.设购买x个甲种文具时,需购买y个乙种文具.
(1)①当减少购买1个甲种文具时,x= ,y= ;②求y与x之间的函数表达式.
(2)已知甲种文具每个5元,乙种文具每个3元,张老师购买这两种文具共用去540元.甲、乙两种文具各购买了多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解全校七年级300名学生的视力情况,骆老师从中抽查了50名学生的视力情况、针对这个问题,下面说法正确的是( )
A. 300名学生是总体B. 每名学生是个体
C. 50名学生的视力情况是所抽取的一个样本D. 这个样本容量是300
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车在依次连通A、B、C三地的公路上行驶,甲车从B地出发匀速向C地行驶,同时乙车人B地出发匀速向A地行驶,到达A地并在A地停留1小时后,调头按原速向C地行驶.在两车行驶的过程中,甲、乙两车与B地的距离y(千米)与行驶时间x(小时)之间的函数图象如图所示,当甲、乙两车相遇时,所用时间为_____小时.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面等式成立的是( )
A.83.5°=83°50′
B.37°12′36″=37.48°
C.24°24′24″=24.44°
D.41.25°=41°15′
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com