
【题目】如图所示的折线是某个函数的图象,根据图象解答下列问题.
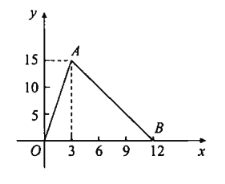
(1)写出自变量x的取值范围:__________,函数值y的取值范围:__________;
(2)求这个分段函数的表达式.
【答案】(1)0≤x≤12;0≤y≤15;(2)y=5x(0≤x≤3),y=![]() x+20(3≤x≤12)
x+20(3≤x≤12)
【解析】
(1)根据函数图象的意义可得出x的取值范围和函数值y的范围;
(2)由图象可求得A、B两点的坐标,利用待定系数法可求出直线AB与OA的解析式.
解:(1)由图象可知自变量x的取值范围为:0≤x≤12,
对应函数值y的取值范围为:0≤y≤15,
(2)由图象得A,B的坐标分别为(3,15),(12,0),![]()
设此一次函数解析式为y=k1x+b1,把A、B两点坐标代入可得![]()
解得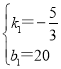
∴直线AB的函数解析式为y=![]() x+20(3≤x≤12)
x+20(3≤x≤12)
设直线OA的函数解析式为y=k2x+b2,把把A、O两点坐标代入可得![]()
解得![]()
∴直线OA的函数解析式为y=5x(0≤x≤3)
故答案为(1)0≤x≤12;0≤y≤15;(2)y=5x(0≤x≤3),y=![]() x+20(3≤x≤12)
x+20(3≤x≤12)


科目:初中数学 来源: 题型:
【题目】如图,△ABC在方格纸中
(1)请在方格纸上建立平面直角坐标系,使A(2,3),C(6,2),并求出B点坐标;
(2)以原点O为位似中心,相似比为2,在第一象限内将△ABC放大,画出放大后的图形△A′B′C′;
(3)计算△A′B′C′的面积S.

查看答案和解析>>
科目:初中数学 来源: 题型:
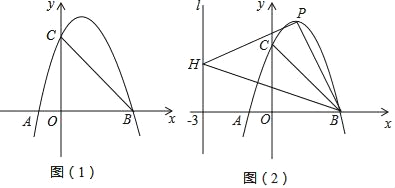
【题目】如图(1),已知抛物线E:y=ax2+bx+c与x轴交于A,B(3,0)两点(A在B的左侧),与y轴交于点C(0,3),对称轴为直线x=1.
(1)填空:a= ,b= ,c= ;
(2)将抛物线E向下平移d个单位长度,使平移后所得抛物线的顶点落在△OBC内(包括△OBC的边界),求d的取值范围;
(3)如图(2),设点P是抛物线E上任意一点,点H在直线x=﹣3上,△PBH能否成为以点P为直角顶点的等腰直角三角形?若能,请求出符合条件的点P的坐标;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BD为⊙O的直径,AB=AC,AD交BC于点E,AE=2,ED=4,
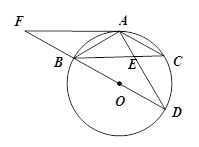
(1)求证:△ABE∽△ADB;
(2)求AB的长;
(3)延长DB到F,使得BF=BO,连接FA,试判断直线FA与⊙O的位置关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店销售A型和B型两种电脑,其中A型电脑每台的利润为400元,B型电脑每台的利润为500元.该商店计划再一次性购进两种型号的电脑共100台,其中B型电脑的进货量不超过A型电脑的2倍,设购进A型电脑x台,这100台电脑的销售总利润为y元.
(1)求y关于x的函数关系式;
(2)该商店购进A型、B型电脑各多少台,才能使销售总利润最大,最大利润是多少?
(3)实际进货时,厂家对A型电脑出厂价下调a(0<a<200)元,且限定商店最多购进A型电脑60台,若商店保持同种电脑的售价不变,请你根据以上信息,设计出使这100台电脑销售总利润最大的进货方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰三角形ABC底边BC的长为4,面积为12,腰AB的垂直平分线EF交AB于点E,交AC于点F.若D为BC边的中点,M为线段EF上一个动点,则△BDM的周长的最小值为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠C=90°,AC=6,AB=10,点D是边BC上一点.若沿AD将△ACD翻折,点C刚好落在AB边上点E处,则AD= _______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明家今年种植的“夏黑”葡萄喜获丰收,采摘上市后若干天便全部销完.小明对销售情况进行了跟踪记录,并将记录情况绘成图象,图中的折线ODE表示日销售量y(千克)与上市时间x(天)之间的函数关系,已知线段DE表示的函数关系中,时间每增加1天,日销售量减少15千克.
(1)第16天的日销售量是 千克.
(2)求y与x之间的函数关系式,并写出x的取值范围;

查看答案和解析>>
科目:初中数学 来源: 题型:
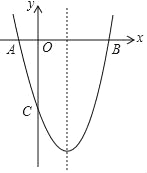
【题目】如图,抛物线y=ax2+bx﹣3(a≠0)与x轴交于A,B两点(点A在点B左侧),与y轴交于点C,且BO=OC=3AO.
(1)求抛物线的解析式;
(2)在抛物线的对称轴上是否存在点P,使△PBC是等腰三角形?若存在,请直接写出符合条件的点P坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com