
分析 如图,作A′H⊥OA于H,根据旋转的性质得OA′=OA=2,∠AOA′=45°,则可判断△OAA′为等腰直角三角形,所以OH=A′H=$\frac{\sqrt{2}}{2}$OA′=$\sqrt{2}$,然后根据第一象限内点的坐标特征写出点A′的坐标.
解答 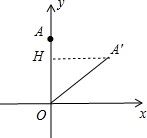 解:如图,作A′H⊥OA于H,
解:如图,作A′H⊥OA于H,
∵点A(0,2)绕着原点O顺时针方向旋转45°角到对应点A′,
∴OA′=OA=2,∠AOA′=45°,
∴△OAA′为等腰直角三角形,
∴OH=A′H=$\frac{\sqrt{2}}{2}$OA′=$\sqrt{2}$,
∴点A′的坐标是($\sqrt{2}$,$\sqrt{2}$).
故答案为($\sqrt{2}$,$\sqrt{2}$).
点评 本题考查了坐标与图形变化-旋转:图形或点旋转之后要结合旋转的角度和图形的特殊性质来求出旋转后的点的坐标.常见的是旋转特殊角度如:30°,45°,60°,90°,180°.


科目:初中数学 来源: 题型:选择题
 如图,点A、B、C、D、E、F为⊙O的六等分点,动点P从圆心O出发,沿OE弧EFFO的路线做匀速运动,设运动的时间为t,∠BPD的度数为y,则下列图象中表示y与t之间函数关系最恰当的是( )
如图,点A、B、C、D、E、F为⊙O的六等分点,动点P从圆心O出发,沿OE弧EFFO的路线做匀速运动,设运动的时间为t,∠BPD的度数为y,则下列图象中表示y与t之间函数关系最恰当的是( )| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
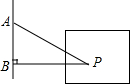 如图,运动会上,小明以直线AB为起跳线,两脚落在点P处,甲乙两名同学测得小明的跳远成绩分别为PA=5.5米,PB=5.1米,则小明的真实成绩为5.1米.
如图,运动会上,小明以直线AB为起跳线,两脚落在点P处,甲乙两名同学测得小明的跳远成绩分别为PA=5.5米,PB=5.1米,则小明的真实成绩为5.1米.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $-\frac{1}{3}$与$-(-\frac{2}{3})$ | B. | -(+7)与+(-7) | C. | -(+2)与(+2.2) | D. | -6与-(-6) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com