
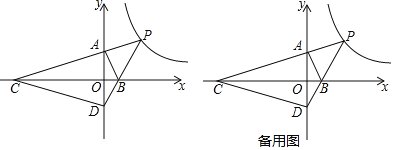
【题目】如图,平面直角坐标系中,O为原点,点A、B分别在y轴、x轴的正半轴上.△AOB的两条外角平分线交于点P,P在反比例函数y![]() 的图象上.PA的延长线交x轴于点C,PB的延长线交y轴于点D,连接CD.
的图象上.PA的延长线交x轴于点C,PB的延长线交y轴于点D,连接CD.
(1)求∠P的度数及点P的坐标;
(2)求△OCD的面积;
(3)△AOB的面积是否存在最大值?若存在,求出最大面积;若不存在,请说明理由.
【答案】(1)∠MPN=90°,P(3,3).(2)9;(3)27﹣18![]() .
.
【解析】
(1)如图,作PM⊥OA于 M,PN⊥OB于N,PH⊥AB于H.利用全等三角形的性质解决问题即可.
(2)设OA=a,OB=b,则AM=AH=3-a,BN=BH=3-b,利用勾股定理求出a,b之间的关系,求出OC,OD即可解决问题.
(3)设OA=a,OB=b,则AM=AH=3-a,BN=BH=3-b,可得AB=6-a-b,推出OA+OB+AB=6,可得![]() ,利用基本不等式即可解决问题.
,利用基本不等式即可解决问题.
解:(1)如图,作PM⊥OA于M,PN⊥OB于N,PH⊥AB于H.
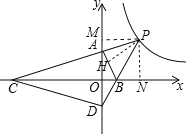
∴∠PMA=∠PHA=90°,
∵∠PAM=∠PAH,PA=PA,
∴△PAM≌△PAH(AAS),
∴PM=PH,∠APM=∠APH,
同理可证:△BPN≌△BPH,
∴PH=PN,∠BPN=∠BPH,
∴PM=PN,
∵∠PMO=∠MON=∠PNO=90°,
∴四边形PMON是矩形,
∴∠MPN=90°,
∴∠APB=∠APH+∠BPH![]() (∠MPH+∠NPH)=45°,
(∠MPH+∠NPH)=45°,
∵PM=PN,
∴可以假设P(m,m),
∵P(m,m)在![]() 上,
上,
∴m2=9,
∵m>0,
∴m=3,
∴P(3,3).
(2)设OA=a,OB=b,则AM=AH=3﹣a,BN=BH=3﹣b,
∴AB=6﹣a﹣b,
∵AB2=OA2+OB2,
∴a2+b2=(6﹣a﹣b)2,
可得ab=6a+6b﹣18,
∴3a+3b﹣9![]() ab,
ab,
∵PM∥OC,
∴![]() ,
,
∴![]() ,
,
∴OC![]() ,同法可得OD
,同法可得OD![]() ,
,
∴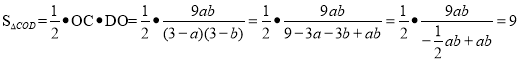 .
.
(3)设OA=a,OB=b,则AM=AH=3﹣a,BN=BH=3﹣b,
∴AB=6﹣a﹣b,
∴OA+OB+AB=6,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴△AOB的面积的最大值为:27﹣18![]() .
.


 优学名师名题系列答案
优学名师名题系列答案科目:初中数学 来源: 题型:
【题目】有一块矩形铁皮,长12dm,宽4dm,在它的四角各切去一个同样的正方形,然后将四周突出部分折起,制作一个无盖方盒,如果要使制作的无盖方盒的侧面积.占矩形铁皮面积的八分之五,设各角切去的正方形的边长为xdm.
(1)用含x的代数式表示,盒底的长为______dm,盒底的宽为______dm;
(2)求x的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为更好地推进太原市生活垃圾分类工作,改善城市生态环境,2019年12月17日,太原市政府召开了太原市生活垃圾分类推进会,意味着太原垃圾分类战役的全面打响.某小区准备购买![]() 两种型号的垃圾箱,通过市场调研得知:购买3个
两种型号的垃圾箱,通过市场调研得知:购买3个![]() 型垃圾箱和2个
型垃圾箱和2个![]() 型垃圾箱共需540元,购买2个
型垃圾箱共需540元,购买2个![]() 型垃圾箱比购买3个
型垃圾箱比购买3个![]() 型垃圾箱少用160元.
型垃圾箱少用160元.

(1)求每个![]() 型垃圾箱和
型垃圾箱和![]() 型垃圾箱各多少元?
型垃圾箱各多少元?
(2)该小区物业计划用不多于2100元的资金购买![]() 两种型号的垃圾箱共20个,则该小区最多可以购买
两种型号的垃圾箱共20个,则该小区最多可以购买![]() 型垃圾箱多少个.
型垃圾箱多少个.
查看答案和解析>>
科目:初中数学 来源: 题型:
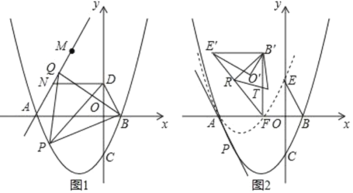
【题目】如图,在平面直角标系中,抛物线C:y=![]() 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,点D为y轴正半轴上一点.且满足OD=
与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,点D为y轴正半轴上一点.且满足OD=![]() OC,连接BD,
OC,连接BD,
(1)如图1,点P为抛物线上位于x轴下方一点,连接PB,PD,当S△PBD最大时,连接AP,以PB为边向上作正△BPQ,连接AQ,点M与点N为直线AQ上的两点,MN=2且点N位于M点下方,连接DN,求DN+MN+![]() AM的最小值
AM的最小值
(2)如图2,在第(1)问的条件下,点C关于x轴的对称点为E,将△BOE绕着点A逆时针旋转60°得到△B′O′E′,将抛物线y=![]() 沿着射线PA方向平移,使得平移后的抛物线C′经过点E,此时抛物线C′与x轴的右交点记为点F,连接E′F,B′F,R为线段E’F上的一点,连接B′R,将△B′E′R沿着B′R翻折后与△B′E′F重合部分记为△B′RT,在平面内找一个点S,使得以B′、R、T、S为顶点的四边形为矩形,求点S的坐标.
沿着射线PA方向平移,使得平移后的抛物线C′经过点E,此时抛物线C′与x轴的右交点记为点F,连接E′F,B′F,R为线段E’F上的一点,连接B′R,将△B′E′R沿着B′R翻折后与△B′E′F重合部分记为△B′RT,在平面内找一个点S,使得以B′、R、T、S为顶点的四边形为矩形,求点S的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如表
x | ﹣1 | 0 | 1 | 3 |
y | ﹣1 | 3 | 5 | 3 |
下列结论:
①ac<0;
②当x>1时,y的值随x值的增大而减小.
③3是方程ax2+(b﹣1)x+c=0的一个根;
④当﹣1<x<3时,ax2+(b﹣1)x+c>0.
其中正确的结论是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
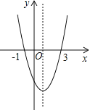
【题目】二次函数![]() 的图象如图所示,给出下列说法:
的图象如图所示,给出下列说法:
①![]() ;②方程
;②方程![]() 的根为
的根为![]() ,
,![]() ;③
;③![]() ;④当
;④当![]() 时,
时,![]() 随
随![]() 值的增大而增大;⑤当
值的增大而增大;⑤当![]() 时,
时,![]() .其中,正确的说法有________(请写出所有正确说法的序号).
.其中,正确的说法有________(请写出所有正确说法的序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】实验数据显示,一般成人喝半斤低度白酒后,1.5 小时内其血液中酒精含量 y(毫克/百毫升) 与时间 x(时)的关系可近似地用二次函数 y=﹣200x2+400x 刻画;1.5 小时后(包括 1.5 小时)y 与 x 可近似地用反比例函数![]()
![]() 刻画(如图所示)
刻画(如图所示)
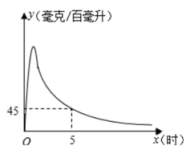
(1)根据上述数学模型计算:喝酒后几时血液中的酒精含量达到最大值?最大值为多少?
(2)按国家规定,车辆驾驶人员血液中的酒精含量大于或等于 20 毫克/百毫升时属于“酒后驾驶”,不能驾车上路.参照上述数学模型,假设某驾驶员晚上 20:00 在家喝完半斤低度白酒,第二天早上 7:00 能否驾车去上班?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年第六届世界互联网大会在乌镇召开,小南和小西参加了某分会场的志愿服务工作,本次志愿服务工作一共设置了三个岗位,分别是引导员、联络员和咨询员.请你用画树状图或列表法求出小南和小西恰好被分配到同一个岗位进行志愿服务的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com