
【题目】ΔABC、ΔCDE都是等边三角形,AD、BE相交于点O,点M、点N分别是线段AD、BE的中点.
(1)证明: AD=BE.(2)求∠DOE的角度。(3)证明:ΔMNC是等边三角形.
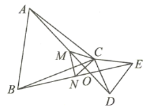
【答案】(1)详见解析;(2)60°;(3)详见解析
【解析】
提示:先证明ΔACD≌BCE(SAS).利用第(1)问证明的结论,用三角形内角和求出∠DOE=60°,易得ΔACM≌ΔBCN(SAS),从而得到ΔCMN为等边三角形.
证明:(1)∵△ABC、△CDE都是等边三角形,
∴AC=BC,CD=CE,∠ACB=∠DCE=60°,
∵∠ACB+∠BCD=∠ACD,
∠DCE+∠BCD=∠BCE,
∴∠ACD=∠BCE,
在△ACD和△BCE中,
AC=BC
∠ACD=∠BCE
CD=CE,
∴△ACD≌△BCE(SAS),
∴AD=BE;
(2)由(1)知∵△ACD≌△BCE,
∴∠ACD=∠BEC,
∵三角形DCE是等边三角形,
∴∠CED=∠CDE=60°
∴∠ADE+∠BED=∠ADC+∠CDE+∠BED=∠ADC+60°+∠BED=∠CED+60°=60°+60°=120°
∴∠DOE=180°-(∠ADE+∠BED)=60°
(3)∵△ACD≌△BCE,
∴∠CAD=∠CBE,
∵点M、N分别是线段AD、BE的中点,AD=BE,
∴AM=BN,
在△ACM和△BCN中,
AC=BC
∠CAD=∠CBE
AM=BN,
∴△ACM≌△BCN(SAS),
∴CM=CN,∠ACM=∠BCN,
∴∠MCN=∠BCM+∠BCN=∠BCM+∠ACM=∠ACB=60°,
∴△MNC是等边三角形.


科目:初中数学 来源: 题型:
【题目】如图,在锐角三角形ABC中,点D,E分别在边AC,AB上,AG⊥BC于点G,AF⊥DE于点F,∠EAF=∠GAC.
(1)求证:△ADE∽△ABC;
(2)若AD=3,AB=5,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数a在数轴上表示的点在原点左侧,距离原点3个单位长,b在数轴上表示的点在原点右侧,距离原点2个单位长,c和d互为倒数,m与n互为相反数,y为最大的负整数,求(y+b)2+m(a-cd)-nb2的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】班级组织同学乘大巴车前往“研学旅行”基地开展爱国教育活动,基地离学校有90公里,队伍8:00从学校出发.苏老师因有事情,8:30从学校自驾小车以大巴1.5倍的速度追赶,追上大巴后继续前行,结果比队伍提前15分钟到达基地.问:
(1)大巴与小车的平均速度各是多少?
(2)苏老师追上大巴的地点到基地的路程有多远?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把正整数1,2,3,4……,排列成如图1所示的一个表,从上到下分别称为第1行、第2行、…,从左到右分别称为第1列、第2列、…….用图2所示的方框在图1中框住16个数,把其中没有被阴影覆盖的四个数分别记为A、B、C、D.设A=x.

(1)在图1中,2018排在第 行第 列;排在第m行第n列的数为 ,其中m≥1,1≤n≤8,且都是正整数;(直接写出答案)
(2)若A+2B+3D=357,求出C所表示的数;
(3)在图(2)中,被阴影覆盖的这些数的和能否为4212?如果能,请求出这些数中最大的数,如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
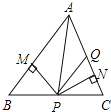
【题目】如图,在不等边![]() 中,
中,![]() ,垂足为M,
,垂足为M,![]() ,垂足为N,且
,垂足为N,且![]() ,点Q在AC上,
,点Q在AC上,![]() ,下列结论:
,下列结论:
![]() ,
,![]()
![]() ,
,![]()
![]() 平分
平分![]() ,
,![]()
![]() 平分
平分![]() ,
,
![]() ≌
≌![]() ,其中正确的个数有()
,其中正确的个数有()
A. 5个B. 4个C. 3个D. 2个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:
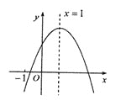
①abc>0;②b>a+c;③9a+3b+c>0; ④c<-3a; ⑤a+b≥m(am+b),其中正确的有( )
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com