
【题目】把正整数1,2,3,4……,排列成如图1所示的一个表,从上到下分别称为第1行、第2行、…,从左到右分别称为第1列、第2列、…….用图2所示的方框在图1中框住16个数,把其中没有被阴影覆盖的四个数分别记为A、B、C、D.设A=x.

(1)在图1中,2018排在第 行第 列;排在第m行第n列的数为 ,其中m≥1,1≤n≤8,且都是正整数;(直接写出答案)
(2)若A+2B+3D=357,求出C所表示的数;
(3)在图(2)中,被阴影覆盖的这些数的和能否为4212?如果能,请求出这些数中最大的数,如果不能,请说明理由.
【答案】(1)253,2;8m+n﹣8;(2)77;(3)这些数的和不能为4212,理由见解析.
【解析】
(1)每行8个数,2018=8×252+2,2018排在第253行第2列;第m行第8列数为8m,第m行第n列为8m+n﹣8;
(2)设A=x,可以依据A、B、C、D四个数排列的规律依次用含x的代数式表达,再根据题意列方程求解即可;
(3)根据题意列方程求出x,如果x为正整数,并且不在第6、7、8列,才能符合题目要求.
解:(1)∵2018=8×252+2,2018排在第253行第2列;根据数字排列规律:第m行最后一列数字为8m,∴排在第m行第n列的数为8m+n﹣8;
故答案为:253,2;8m+n﹣8;
(2)由题意得:A=x,B=x+24,C=x+27,D=x+3,
∵A+2B+3D=357,
∴x+2(x+24)+3(x+3)=357,
解得:x=50,
∴C=x+27=50+27=77.
(3)这些数的和不能为4212;
∵被阴影覆盖的这些数的和=x+1+x+2+x+8+x+9+x+10+x+11+x+16+x+17+x+18+x+19+x+25+x+26=12x+162
若12x+162=4212,则x=337.5不是正整数,不符合题意.
故答案为:(1)253,2;8m+n﹣8;(2)77;(3)这些数的和不能为4212,理由见解析.


科目:初中数学 来源: 题型:
【题目】已知在△ABC中,AB=AC,AB的垂直平分线交线段AC于D,若△ABC和△DBC的周长分别是60 cm和38 cm,则△ABC的腰长和底边BC的长分别是( )
A. 22cm和16cmB. 16cm和22cm
C. 20cm和16cmD. 24cm和12cm
查看答案和解析>>
科目:初中数学 来源: 题型:
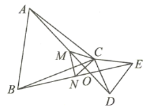
【题目】ΔABC、ΔCDE都是等边三角形,AD、BE相交于点O,点M、点N分别是线段AD、BE的中点.
(1)证明: AD=BE.(2)求∠DOE的角度。(3)证明:ΔMNC是等边三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 是
是![]() 的高.
的高.
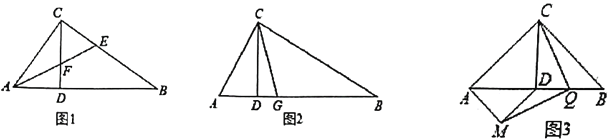
(1)如图1,若![]() ,
,![]() 的平分线
的平分线![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,求证:
,求证:![]() ;
;
(2)如图2,若![]() ,
,![]() 的平分线
的平分线![]() 交
交![]() 于点
于点![]() ,求
,求![]() 的值;
的值;
(3)如图3,若![]() 是以
是以![]() 为斜边的等腰直角三角形,再以
为斜边的等腰直角三角形,再以![]() 为斜边作等腰
为斜边作等腰![]() ,
,![]() 是
是![]() 的中点,连接
的中点,连接![]() 、
、![]() ,试判断线段
,试判断线段![]() 与
与![]() 的关系,并给出证明.
的关系,并给出证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车分别从A,B两地同时出发相向而行.并以各自的速度匀速行驶,甲车途径C地时休息一小时,然后按原速度继续前进到达B地;乙车从B地直接到达A地,如图是甲、乙两车和B地的距离y(千米)与甲车出发时间x(小时)的函数图象.

(1)直接写出a,m,n的值;
(2)求出甲车与B地的距离y(千米)与甲车出发时间x(小时)的函数关系式(写出自变量x的取值范围);
(3)当两车相距120千米时,乙车行驶了多长时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表是某校九年级(1)班20名学生某次数学测验的成绩统计表:
成绩(分) | 60 | 70 | 80 | 90 | 100 |
人数(人) | 1 | 5 | x | y | 2 |
(1)若这20名学生成绩的平均分数为82分,求x和y的值;
(2)在(1)的条件下,设这20名学生本次测验成绩的众数为a,中位数为b,求a,b的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系 xOy 中,点A,B的坐标分别为(-2,0),(1,0).同时将点A ,B先向左平移1个单位长度,再向上平移2个单位长度,得到点A,B的对应点依次为C,D,连接CD,AC, BD .
(1)写出点C , D 的坐标;
(2)在 y 轴上是否存在点E,连接EA ,EB,使S△EAB=S四边形ABDC?若存在,求出点E的坐标;若不存在,说明理由;
(3)点 P 是线段 AC 上的一个动点,连接 BP , DP ,当点 P 在线段 AC 上移动时(不与 A , C 重合),直接写出CDP 、ABP 与BPD 之间的等量关系.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com