
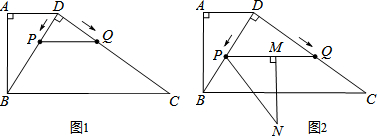
���� ��1������֤����ABD�ס�DCB���������������εĶ�Ӧ�ߵı�������BD�ij���
��2������x��ʾ��DP��DQ�ij���֤����BCD�ס�PQD�����DPQ=��DBC������ƽ���ߵ��ж�����֤����
��3������PE��BC�ڵ�E����PE=DQ�ǣ�N��BC�ϣ����x��ֵ��Ȼ��ֳ�N��BC��ǰ��N��BC�±���������������ۣ��Ӷ���⣻
��������Ʒֳ���������������в���ʽ�Ӷ���⣮
��� �⣺��1����AD��BC��
���ADB=��DBC��
�֡ߡ�A=��BDC=90�㣬
���ABD�ס�DCB��
��$\frac{AD}{DB}=\frac{DB}{BC}$����$\frac{\frac{9}{5}}{DB}=\frac{DB}{5}$��
��ã�BD=3��
��2����ֱ�ǡ�BCD�У�CD=$\sqrt{B{C}^{2}-B{D}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4��
DP=xcm��DQ=$\frac{4}{3}$xcm��
��$\frac{DP}{DB}=\frac{DQ}{CD}$��
�֡ߡ�BDC=��PDQ��
���BCD�ס�PQD��
���DPQ=��DBC��
��PQ��BC��
��3����PE��BC�ڵ�E��
���PBE�ס�CBD��$\frac{PE}{CD}=\frac{BP}{BC}$����$\frac{PE}{4}=\frac{3-x}{5}$����PE=$\frac{4}{5}$��3-x����
ͬ����DQ=$\frac{4}{3}$PD=$\frac{4}{3}$x��PQ=$\frac{5}{3}$x��
����N����BC����ʱ$\frac{4}{5}$��3-x��=$\frac{4}{3}x$��
��ã�x=$\frac{9}{8}$��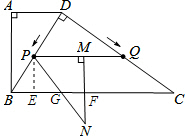
�ٵ�0��x��$\frac{9}{8}$ʱ��y=x+$\frac{4}{3}$x+$\frac{5}{3}$x=4x��
��$\frac{9}{8}$��x��3ʱ��FN=MN-MF=DQ-PE=$\frac{4}{3}$x-$\frac{4}{5}$��3-x��=$\frac{32}{15}$x-$\frac{12}{5}$��
����ֱ�ǡ�NFG�У�FG=$\frac{3}{4}$FN=$\frac{3}{4}$��$\frac{32}{15}$x-$\frac{12}{5}$��=$\frac{8}{5}$x-$\frac{9}{5}$��
GN=$\frac{5}{4}$x=$\frac{5}{4}$��$\frac{32}{15}$x-$\frac{12}{5}$��=$\frac{8}{3}$x-3��
��PG=$\frac{5}{3}$x-��$\frac{8}{3}$x-3��=3-x��
��y=x+$\frac{4}{5}$��3-x��+��$\frac{8}{5}$x-$\frac{9}{5}$��+��3-x��=$\frac{4}{5}$x+$\frac{18}{5}$��
�ڵ�0��x��$\frac{9}{8}$ʱ��4��4x��5ʱ����ã�1��x��$\frac{5}{4}$����1��x��$\frac{9}{8}$��
��$\frac{9}{8}$��x��3��4��$\frac{4}{5}$x+$\frac{18}{5}$��5ʱ����ã�$\frac{1}{2}$��x��$\frac{7}{4}$����$\frac{9}{8}$��x��$\frac{7}{4}$��
��֮��1��x��$\frac{7}{4}$��
���� ���⿼�������������ε��ж������ʣ��������������ε����ʣ���ȷ����x��ʾ��ͼ�����߶�GN��PG��DQ�ij����ǹؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
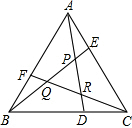 ��ABCΪ�������Σ�D��E��F���ȷ�BC��AC��AB����ͼ����S��PQR��S��ABC=$\frac{1}{7}$��
��ABCΪ�������Σ�D��E��F���ȷ�BC��AC��AB����ͼ����S��PQR��S��ABC=$\frac{1}{7}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 y24-2��
y24-2��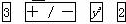 =607��
=607���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x��2-$\sqrt{2}$ | B�� | x��2$\sqrt{2}$-1 | C�� | x��2 | D�� | x��$\sqrt{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
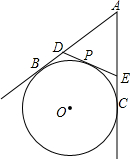 ��֪����ͼ��AB��AC�ǡ�O�����ߣ�B��C���е㣬��$\widehat{BC}$�ϵ�����һ��P����O��������AB��AC�ֱ��ڵ�D��E��
��֪����ͼ��AB��AC�ǡ�O�����ߣ�B��C���е㣬��$\widehat{BC}$�ϵ�����һ��P����O��������AB��AC�ֱ��ڵ�D��E���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
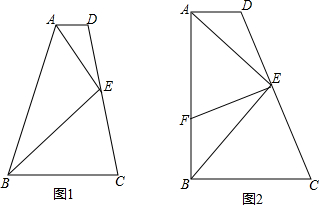
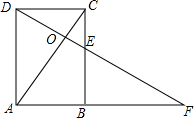 �ھ���ABCD�У���F��BC����һ�㣬��DE���ӳ���AB���ӳ�����F������AC��DF�ڵ�O
�ھ���ABCD�У���F��BC����һ�㣬��DE���ӳ���AB���ӳ�����F������AC��DF�ڵ�O�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com