
【题目】如图,点A,B分别在x轴、y轴上,点O关于AB的对称点C在第一象限,将△ABC沿x轴正方向平移k个单位得到△DEF(点B与E是对应点),点F落在双曲线y=![]() 上,连结BE交该双曲线于点G.∠BAO=60°,OA=2GE,则k的值为 ________ .
上,连结BE交该双曲线于点G.∠BAO=60°,OA=2GE,则k的值为 ________ .

【答案】![]()
【解析】
设OA等于2m, 由对称图形的特点,和勾股定理等把C点和B点坐标用含m的代数式来表示,F、E、G是由△ABC平移K个单位得到,坐标可以用含m和k的代数式表示,因为G、F在双曲线上,所以其横纵坐标的乘积都为k,据此列两个关系式,先求出m的值,从而可求k的值.
如图:作CH垂直于x轴,CK垂直于y轴,
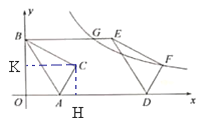
由对称图形的特点知,CA=OA, 设OA=2m,
∵∠BAO=60°,
∴OB=2![]() ,AC=2m, ∠CAH=180°-60°-60°=60°,
,AC=2m, ∠CAH=180°-60°-60°=60°,
∴AH=m,CH=![]() ,
,
∴C点坐标为(3m, ![]() ),
),
则F点坐标为(3m+k, ![]() ),
),
F点在双曲线上,则(3m+k)×![]() =k,
=k,
B点坐标为(0,2![]() ),
),
则E点坐标为(k,2![]() ),
),
G点坐标为(k-m,2![]() ),
),
则(k-m) × 2![]() m=k,
m=k,
∴(3m+k)×![]() m=(k-m) ×2
m=(k-m) ×2![]() m,
m,
整理得k=5m,代入(k-m)2![]() m=k中,
m=k中,
得4m×2![]() m=5m,
m=5m,
即m=0(舍去),m=![]() ,
,
则![]() ,
,
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=5cm,BC=10cm,动点M从点D出发,按折线DCBAD方向以3cm/s的速度运动,动点N从点D出发,按折线DABCD方向以2cm/s的速度运动.点E在线段BC上,且BE=1cm,若M、N两点同时从点D出发,到第一次相遇时停止运动.
(1)求经过几秒钟M、N两点停止运动?
(2)求点A、E、M、N构成平行四边形时,M、N两点运动的时间;
(3)设运动时间为t(s),用含字母t的代数式表示△EMN的面积S(cm2).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点D在⊙O的直径AB的延长线上,点C在⊙O上,AC=CD,∠ACD=120°.
(1)求证:CD是⊙O的切线;
(2)若⊙O的半径为2,求图中阴影部分的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=24厘米,BC=16厘米,点D为AB的中点,点P在线段BC上以4厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.当点Q的运动速度为_______厘米/秒时,能够在某一时刻使△BPD与△CQP全等.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,若二次函数![]() 的图象与x轴交于点A(-2,0),B(3,0)两点,点A关于正比例函数
的图象与x轴交于点A(-2,0),B(3,0)两点,点A关于正比例函数![]() 的图象的对称点为C。
的图象的对称点为C。
(1)求b、c的值;
(2)证明:点C 在所求的二次函数的图象上;
(3)如图②,过点B作DB⊥x轴交正比例函数![]() 的图象于点D,连结AC,交正比例函数
的图象于点D,连结AC,交正比例函数![]() 的图象于点E,连结AD、CD。如果动点P从点A沿线段AD方向以每秒2个单位的速度向点D运动,同时动点Q从点D沿线段DC方向以每秒1个单位的速度向点C运动,当其中一个到达终点时,另一个随之停止运动,连结PQ、QE、PE,设运动时间为t秒,是否存在某一时刻,使PE平分∠APQ,同时QE平分∠PQC,若存在,求出t的值;若不存在,请说明理由。
的图象于点E,连结AD、CD。如果动点P从点A沿线段AD方向以每秒2个单位的速度向点D运动,同时动点Q从点D沿线段DC方向以每秒1个单位的速度向点C运动,当其中一个到达终点时,另一个随之停止运动,连结PQ、QE、PE,设运动时间为t秒,是否存在某一时刻,使PE平分∠APQ,同时QE平分∠PQC,若存在,求出t的值;若不存在,请说明理由。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与双曲线相交于点A(m,3),与x轴交于点C.
与双曲线相交于点A(m,3),与x轴交于点C.
(1)求双曲线解析式;
(2)点P在x轴上,如果△ACP的面积为3,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C在线段AB上,过点C作CD⊥AB,点E,F分别是AD,CD的中点,连结EF并延长EF至点G,使得FG=CB,连结CE,GB,过点B作BH∥CE交线段EG于点H.
(1)求证:四边形FCBG是矩形.
(2)己知AB=10,![]() .
.
①当四边形ECBH是菱形时,求EG的长.
②连结CH,DH,记△DEH的面积为S1, △CBH的面积为S2.若EG=2FH,求S1+S2的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:四边形ABCD,E,F,G,H是各边的中点.
(1)求证:四边形EFGH是平行四边形;
(2)假如四边形ABCD是一个矩形,猜想四边形EFGH是什么图形?并证明你的猜想.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电业局要对某市区的电线路进行巡检,某检修小组从A地出发,在东西向的马路上检修线路,如果规定向东行驶为正,向西行驶为负,检修车一天中八次行驶记录如下:(单位:km)-4,+7,-9,+8,+6,-5,-2,-4
(1)求收工时检修小组在A地的什么方向?距A地多远?
(2)若每千米耗油0.5升,当维修小组返回到A地时,问共耗油多少升?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com