
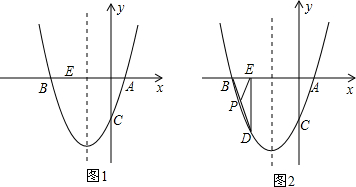
���� ��1�����ô���ϵ����������ö��κ����Ľ���ʽ��
��2���������ۣ���GH��ACʱ����ͼ1��a������A����C��GH�ľ�����ȣ���S��GHC=S��GHA�������ô���ϵ�������AC�Ľ���ʽΪy=3x-3����������ֱ��ƽ���������GH�Ľ���ʽΪy=3x-1��Ȼ��ͨ���ⷽ����$\left\{\begin{array}{l}{y={x}^{2}+2x-3}\\{y=3x-1}\end{array}\right.$�õ�G��-1��-4������GH��AC��ƽ��ʱ����ͼ1��b������ȷ��AC���е�ΪM��$\frac{1}{2}$��-$\frac{3}{2}$�������ڵ�A��C��ֱ��GH�ľ�����ȣ���GH����Mʱ��S��GHC=S��GHA�����ô���ϵ�������ֱ��HM�Ľ���ʽΪy=-x-1����ͨ���ⷽ����$\left\{\begin{array}{l}{y={x}^{2}+2x-3}\\{y=-x-1}\end{array}\right.$��G��$\frac{-3-\sqrt{17}}{2}$��$\frac{1+\sqrt{17}}{2}$����
��3������ͼ2��ȡ��E����y��ĶԳƵ�N����N��2��0��������DN��y����F����FE=FN����������֮���߶�����жϴ�ʱ��EDF���ܳ���С������ȷ��D��-2��-3��������OF��DE����F��ΪDN���е㣬����F��0��-$\frac{3}{2}$����
�ڸ���������������ʵá�BPE+��EPF=��FDP+��PFD������EPF=��FDP�����BPE=��PFD���ټ����DN=BN=5���õ���BND=��NDB�����ǿ��жϡ�PBE�ס�FDP���������Ʊȿɵ�PB•DP=$\frac{5}{2}$������BP+DP=BD=$\sqrt{10}$�����ýⷽ����ɵ�PB=$\frac{\sqrt{10}}{2}$�����Ե�PΪBD���е㣬Ȼ���ж�PFΪ��DBN����λ�ߣ���������������λ��������⣮
��� �⣺��1����A��1��0����C��0��-3������y=ax2+2x+c��$\left\{\begin{array}{l}{1=a+2+c}\\{c=-3}\end{array}\right.$��
���$\left\{\begin{array}{l}{a=1}\\{c=-3}\end{array}\right.$����
���������߽���ʽΪy=x2+2x-3��
��2�����ڣ�
��GH��ACʱ����ͼ1��a������A����C��GH�ľ�����ȣ�
��S��GHC=S��GHA��
��AC�Ľ���ʽΪy=3x-3����HG�Ľ���ʽΪy=3x+b��
��H��0��-1�������b=-1��
��GH�Ľ���ʽΪy=3x-1��
�ɵ÷�����$\left\{\begin{array}{l}{y={x}^{2}+2x-3}\\{y=3x-1}\end{array}\right.$��
���$\left\{\begin{array}{l}{x=-1}\\{y=-4}\end{array}\right.$��$\left\{\begin{array}{l}{x=2}\\{y=5}\end{array}\right.$��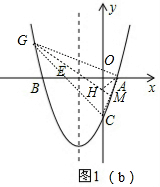
��G��-1��-4����
��GH��AC��ƽ��ʱ����ͼ1��b��AC���е�ΪM��$\frac{1}{2}$��-$\frac{3}{2}$����
�ߵ�A��C��ֱ��GH�ľ�����ȣ�
��GH����Mʱ��S��GHC=S��GHA��
��ֱ��HM�Ľ���ʽΪy=px+q��
��H��0��-1����M��$\frac{1}{2}$��-$\frac{3}{2}$�������$\left\{\begin{array}{l}{q=-1}\\{\frac{1}{2}p+q=-\frac{3}{2}}\end{array}\right.$�����$\left\{\begin{array}{l}{p=-1}\\{q=-1}\end{array}\right.$��
��ֱ��HM�Ľ���ʽΪy=-x-1��
�ⷽ����$\left\{\begin{array}{l}{y={x}^{2}+2x-3}\\{y=-x-1}\end{array}\right.$��$\left\{\begin{array}{l}{x=\frac{-3+\sqrt{17}}{2}}\\{y=\frac{1-\sqrt{17}}{2}}\end{array}\right.$��$\left\{\begin{array}{l}{x=\frac{-3-\sqrt{17}}{2}}\\{y=\frac{1+\sqrt{17}}{2}}\end{array}\right.$��
��G��$\frac{-3-\sqrt{17}}{2}$��$\frac{1+\sqrt{17}}{2}$����
��������������������P��������-1��-4������$\frac{-3-\sqrt{17}}{2}$��$\frac{1+\sqrt{17}}{2}$����
��3������ͼ2��ȡ��E����y��ĶԳƵ�N����N��2��0����
����DN��y����F����FE=FN��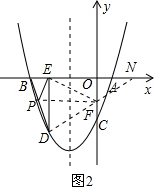 ��FE+FD=FN+DF=DN��
��FE+FD=FN+DF=DN��
���ʱ��EDF���ܳ���С��
��E��-2��0����DE��x�ᣬ
��D�ĺ�����Ϊ-2��
��D��-2��-3����
��OF��DE��
��F��ΪDN���е㣬
��F��0��-$\frac{3}{2}$����
�ڡߡ�BPF=��BDF+��PFD��
����BPE+��EPF=��FDP+��PFD��
����EPF=��FDP��
���BPE=��PFD��
��DN=$\sqrt{{4}^{2}+{3}^{2}}$=5��BN=2+3=5��
��NB=ND��
���BND=��NDB��
���PBE�ס�FDP��
��$\frac{PB}{FD}$=$\frac{BE}{DP}$����$\frac{PB}{\frac{5}{2}}$=$\frac{1}{DP}$��
��PB•DP=$\frac{5}{2}$��
��BP+DP=BD=$\sqrt{��-2+3��^{2}+{3}^{2}}$=$\sqrt{10}$��
��PB��$\sqrt{10}$-PB��=$\frac{5}{2}$��
������PB2-$\sqrt{10}$PB+$\frac{5}{2}$=0�����PB=$\frac{\sqrt{10}}{2}$��
���PΪBD���е㣬
��F��ΪDN���е㣬
��PFΪ��DBN����λ�ߣ�
��PF=$\frac{1}{2}$BN=$\frac{5}{2}$��
���� ���⿼���˶��κ������ۺ��⣺�����ô���ϵ��������κ����Ľ���ʽ������ֱ������κ����Ľ������������������������ۺ��Ժ�ǿ���ѶȽϴ���Ĺؼ���ע�����ν��˼�롢��������˼���뷽��˼���Ӧ�ã�


 ��ɢ˼ά�¿���ϵ�д�
��ɢ˼ά�¿���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� |  | B�� | 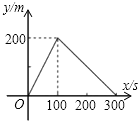 | C�� | 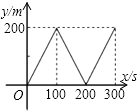 | D�� | 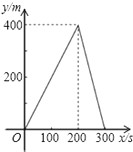 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
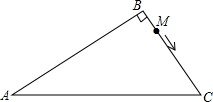 ��ͼ����Rt��ABC�У���B=90�㣬AB=2$\sqrt{3}$cm��AC=4cm������M�ӵ�B������ÿ��$\sqrt{2}$cm���ٶ���B��C��A�����ƶ�����A�����M���������ʹ��ABC������ǡ�ABM�����4����
��ͼ����Rt��ABC�У���B=90�㣬AB=2$\sqrt{3}$cm��AC=4cm������M�ӵ�B������ÿ��$\sqrt{2}$cm���ٶ���B��C��A�����ƶ�����A�����M���������ʹ��ABC������ǡ�ABM�����4�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
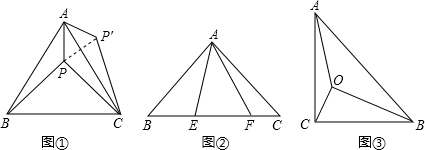
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
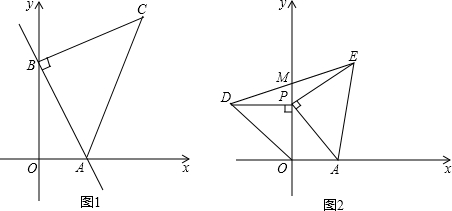
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
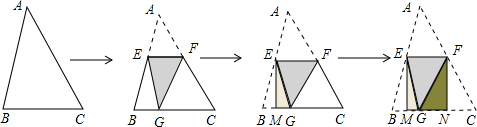
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com