
| A. | 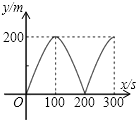 | B. | 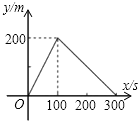 | C. | 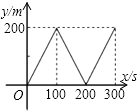 | D. | 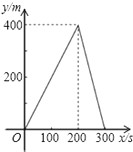 |
分析 由于同向而行,且二人速度差为6-4=2m/s,二人间最长距离为200米,最短距离为0,据此即可进行推理.
解答 解:二人速度差为6-4=2m/s,
100秒时,二人相距2×100=200米,
200秒时,二人相距2×200=400米,较短部分的长度为0,
300秒时,二人相距2×300=600米,即甲超过乙600-400=200米.
由于y=2x(0≤x≤100)或y=400-2x(100≤x≤200)或y=2x-400(200≤x≤300),函数图象为直线(线段).
故选:C.
点评 本题考查了利用函数的图象解决实际问题,正确理解函数图象表示的意义,理解问题的过程,就能够通过图象得到函数问题的相应解决.


 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
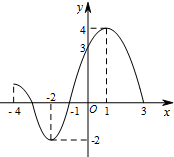 已知某函数图象如图所示,请回答下列问题:
已知某函数图象如图所示,请回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
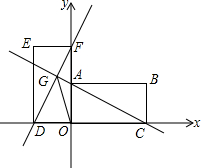 如图,直线y=-$\frac{1}{2}$x+1交y轴于A点,交x轴于C点,以A,O,C为顶点作矩形AOCB,将矩形AOCB绕O点逆时针旋转90°,得到矩形DOFE,直线AC交直线DF于G点.
如图,直线y=-$\frac{1}{2}$x+1交y轴于A点,交x轴于C点,以A,O,C为顶点作矩形AOCB,将矩形AOCB绕O点逆时针旋转90°,得到矩形DOFE,直线AC交直线DF于G点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
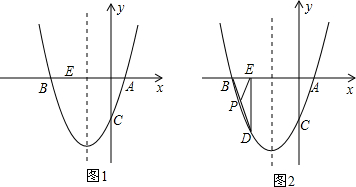
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com