练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】①将下列各数填入相应的括号中:

    0,-2019，7.01,+6,+30﹪,

    负数:{ }

    正数:{ }

    整数:{ }

    ②.画一条数轴，在数轴上标出以下各点，然后用“＜”符号连起来.

    -；-（-4）；-|-1|；；0；；2.5；

    【答案】（1）见解析；（2）见解析.

    【解析】

    ①根据正、负数和整数的定义进行分类；

    ②把各数表示在数轴上，根据借助数轴比较有理数大小的方法，用“＜”连接各数即可．

    ①0，-2019，7.01，+6，+30%，数中，

    负数有：-2019，；

    正数有7.01，+6，+30%；

    整数有：0，-2019，+6．

    ②∵-（-4）=4，-|-1|=-1，（-1）2=1，-22=-4．

    ∴-22＜-＜-|-1|＜0＜（-1）2＜2.5＜-（-4）．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】数轴上两点间的距离等于这两个点所对应的数的差的绝对值．例：点A、B在数轴上对应的数分别为a、b，则A、B两点间的距离表示为AB＝|a﹣b|．根据以上知识解题：

    （1）点A在数轴上表示3，点B在数轴上表示2，那么AB＝_______．

    （2）在数轴上表示数a的点与﹣2的距离是3，那么a＝______．

    （3）如果数轴上表示数a的点位于﹣4和2之间，那么|a+4|+|a﹣2|＝______．

    （4）对于任何有理数x，|x﹣3|+|x﹣6|是否有最小值？如果有，直接写出最小值．如果没有．请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】垫球是排球队常规训练的重要项目之一．下列图表中的数据是甲、乙、丙三人每人十次垫球测试的成绩．测试规则为连续接球10个，每垫球到位1个记1分．

    运动员甲测试成绩表

    测试序号

    1

    2

    3

    4

    5

    6

    7

    8

    9

    10

    成绩（分）

    7

    6

    8

    7

    7

    5

    8

    7

    8

    7

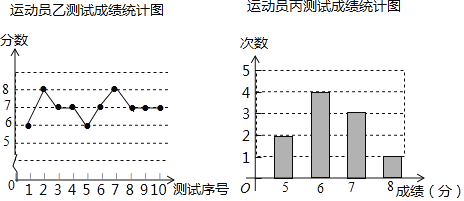
    （1）写出运动员甲测试成绩的众数和中位数；

    （2）在他们三人中选择一位垫球成绩优秀且较为稳定的接球能手作为自由人，你认为选谁更合适?为什么? (参考数据：三人成绩的方差分别为、、)

    （3）甲、乙、丙三人相互之间进行垫球练习，每个人的球都等可能的传给其他两人，球最先从甲手中传出，第三轮结束时球回到甲手中的概率是多少？（用树状图或列表法解答）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为了丰富课外活动，某校将购买一些乒乓球拍和乒乓球，某商场销售一种乒乓球拍和乒乓球，乒乓球拍每副定价80元，乒乓球每盒定价20元，“国庆节”期间商场决定开展促销活动，活动期间向客户提供两种优惠方案.

    方案一：买一副乒乓球拍送一盒乒乓球；

    方案二：乒乓球拍和乒乓球都按定价的90%付款．

    某校要到该商场购买乒乓球拍20副，乒乓球盒(>20且为整数)．

    （1）若按方案一购买，需付款 元(用含的整式表示，要化简)； 若按方案二购买，需付款 元(用含的整式表示，要化简).

    （2）若30，通过计算说明此时按哪种方案购买较为合算？

    （3）当30时，你能给出一种更为省钱的购买方案吗？试写出你的购买方法．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在Rt△ABC中， 点P从点A出发，沿折线AB-BC向终点C运动，在AB上以每秒8个单位长度的速度运动，在BC上以每秒2个单位长度的速度运动.动点Q从点C出发，沿CA方向以每秒个单位长度的速度运动.P、Q两点同时出发，当点P停止时，点Q也随之停止.设点P的运动时间为t秒.

    （1）用含t的代数式表示线段AQ的长.

    （2）当点P在线段AB上运动时，求PQ与△ABC一边垂直时t的值.

    （3）设△APQ的面积为S（S>0），求S与t的函数关系式.

    （4）当△APQ是以PQ为腰的等腰三角形时,直接写出t的值.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】图1是一段圆柱体的树干的示意图，已知树干的半径r=10cm，AD=45cm. （π值取3）

    （1）若螳螂在点A处，蝉在点C处，图1中画出了螳螂捕蝉的两条路线，即A→D→C和A→C，图2是该圆柱体的侧面展开图，判断哪条路的距离较短，并说明理由；

    （2）若螳螂在点A处，蝉在点D处，螳螂想要捕到这只蝉，但又怕蝉发现，于是螳螂绕到

    后方去捕捉它，如图3所示，求螳螂爬行的最短距离；（提示： =75）

    （3）图4是该圆柱体的侧面展开图，蝉N在半径为10cm的⊙O的圆上运动，⊙O与BC相切，点O到CD的距离为20cm，螳螂M在线段AD运动上，连接MN，MN即为螳螂捕蝉时螳螂爬行的距离，若要使MN与⊙O总是相切，求MN的长度范围.

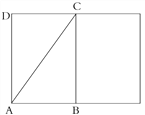
    图1 图2 图3 图4

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知，如图，AB∥CD，直线EF分别交AB、CD于点E、F，EG平分∠AEF，FH平分∠EFD．求证：EG∥FH．

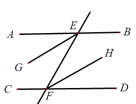
    请完成以下证明过程：

    证明：∵AB∥CD(已知)

    ∴∠AEF=∠EFD（__________________）

    ∵EG平分∠AEF，FH平分∠EFD（__________）

    ∴∠___＝∠AEF,∠___= ∠EFD（____________）

    ∴∠_____=∠______(等量代换)

    ∴EG∥FH（__________________）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系xOy中，直线l1：y＝x+b与x轴交于点A，与y轴交于点B，且点C的坐标为（4，﹣4）．

    （1）点A的坐标为　 　，点B的坐标为　 　；（用含b的式子表示）

    （2）当b＝4时，如图所示．连接AC，BC，判断△ABC的形状，并证明你的结论；

    （3）过点C作平行于y轴的直线l2，点P在直线l2上．当﹣5＜b＜4时，在直线l1平移的过程中，若存在点P使得△ABP是以AB为直角边的等腰直角三角形，请直接写出所有满足条件的点P的纵坐标．

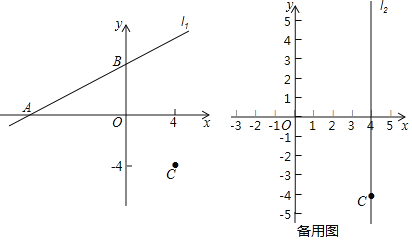
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（1）已知一次函数的图象经过，两点.求这个一次函数的解析式；并判断点是否在这个一次函数的图象上；

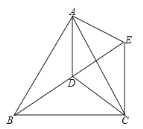
    （2）如图所示，点D是等边内一点，，，，将绕点A逆时针旋转到的位置，求的周长．

    查看答案和解析>>

    同步练习册答案