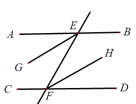
【题目】已知，如图，AB∥CD，直线EF分别交AB、CD于点E、F，EG平分∠AEF，FH平分∠EFD．求证：EG∥FH．
请完成以下证明过程：
证明：∵AB∥CD(已知)
∴∠AEF=∠EFD（__________________）
∵EG平分∠AEF，FH平分∠EFD（__________）
∴∠___＝
∠AEF,∠___= ∠EFD（____________）
∴∠_____=∠______(等量代换)
∴EG∥FH（__________________）．
科目：初中数学 来源： 题型：
【题目】（观察探索）用“＜”、“＞”或“=”完成以下填空，并观察两边算式，探索规律:
（猜想证明）请用一个含字母a、b的式子表示上以规律，并证明结论的正确性；
（应用拓展）比较代数式m2-3mn+1与mn-4n2的大小，并说明理由.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】①将下列各数填入相应的括号中:
0,-2019，7.01,+6,+30﹪,
负数:{ }
正数:{ }
整数:{ }
②.画一条数轴，在数轴上标出以下各点，然后用“＜”符号连起来.
-
；-（-4）；-|-1|；
；0；
；2.5；
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，抛物线
与两轴分别交于A、B、C三点，已知点A（一3，O），B(1，0)．点P在第二象限内的抛物线上运动，作PD上
轴子点D，交直线AC于点E．
(1) 
(2)过点P作PF⊥AC于点F．求当△PEF的周长取最大值时点P的坐标．
(3)连接AP，并以AP为边作等腰直角△APQ，当顶点Q恰好落在抛物线的对称轴上时，求对应的P点坐标.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】用正方形硬纸板做三棱柱盒子，每个盒子由3个矩形侧面和2个正三角形底面组成。硬纸板以如图两种方式裁剪（裁剪后边角料不再利用）
A方法：剪6个侧面； B方法：剪4个侧面和5个底面。
现有19张硬纸板，裁剪时
张用A方法，其余用B方法。
（1）用的代数式分别表示裁剪出的侧面和底面的个数；
（2）若裁剪出的侧面和底面恰好全部用完，问能做多少个盒子？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知，如图，AB∥CD，直线EF分别交AB、CD于点E、F，EG平分∠AEF，FH平分∠EFD．求证：EG∥FH．
请完成以下证明过程：
证明：∵AB∥CD(已知)
∴∠AEF=∠EFD（__________________）
∵EG平分∠AEF，FH平分∠EFD（__________）
∴∠___＝
∠AEF,∠___= ∠EFD（____________）
∴∠_____=∠______(等量代换)
∴EG∥FH（__________________）．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】把下列各数填入相应集合的括号内.
+6.5，
，0.5，0，-3.2，13，-9，
，-1，-3.6
（1）正数集合：{ …}；
（2）整数集合：{ …}；
（3）非负数集合：{ …}；
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
