
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕxOyжаЃЌжБЯпl1ЃКyЃН![]() x+bгыxжсНЛгкЕуAЃЌгыyжсНЛгкЕуBЃЌЧвЕуCЕФзјБъЮЊЃЈ4ЃЌЉ4ЃЉЃЎ
x+bгыxжсНЛгкЕуAЃЌгыyжсНЛгкЕуBЃЌЧвЕуCЕФзјБъЮЊЃЈ4ЃЌЉ4ЃЉЃЎ
ЃЈ1ЃЉЕуAЕФзјБъЮЊЁЁ ЁЁЃЌЕуBЕФзјБъЮЊЁЁ ЁЁЃЛЃЈгУКЌbЕФЪНзгБэЪОЃЉ
ЃЈ2ЃЉЕБbЃН4ЪБЃЌШчЭМЫљЪОЃЎСЌНгACЃЌBCЃЌХаЖЯЁїABCЕФаЮзДЃЌВЂжЄУїФуЕФНсТлЃЛ
ЃЈ3ЃЉЙ§ЕуCзїЦНаагкyжсЕФжБЯпl2ЃЌЕуPдкжБЯпl2ЩЯЃЎЕБЉ5ЃМbЃМ4ЪБЃЌдкжБЯпl1ЦНвЦЕФЙ§ГЬжаЃЌШєДцдкЕуPЪЙЕУЁїABPЪЧвдABЮЊжБНЧБпЕФЕШбќжБНЧШ§НЧаЮЃЌЧыжБНгаДГіЫљгаТњзуЬѕМўЕФЕуPЕФзнзјБъЃЎ
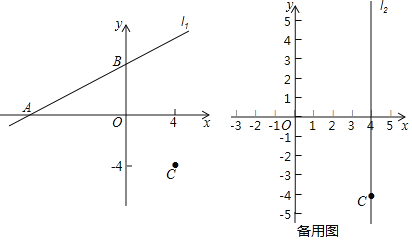
ЁОД№АИЁПЃЈ1ЃЉЃЈЉ2bЃЌ0ЃЉЃЌЃЈ0ЃЌbЃЉЃЛЃЈ2ЃЉЁїABCЪЧЕШбќжБНЧШ§НЧаЮЃЌРэгЩМћНтЮіЃЛЃЈ3ЃЉДцдкЃЌТњзуЬѕМўЕФЕуPзјБъЮЊЃЈ4ЃЌЉ![]() ЃЉЛђЃЈ4ЃЌ8ЃЉЛђЃЈ4ЃЌЉ12ЃЉЃЌРэгЩМћНтЮі
ЃЉЛђЃЈ4ЃЌ8ЃЉЛђЃЈ4ЃЌЉ12ЃЉЃЌРэгЩМћНтЮі
ЁОНтЮіЁП
ЃЈ1ЃЉгЩД§ЖЈЯЕЪ§ЗЈМДПЩНтОіЮЪЬтЃЛ
ЃЈ2ЃЉЁїABCЪЧЕШбќжБНЧШ§НЧаЮЃЎИљОнСНЕуМфОрРыЙЋЪНвдМАЙДЙЩЖЈРэЕФФцЖЈРэМДПЩХаЖЯЃЛ
ЃЈ3ЃЉЗжШ§жжЧщаЮЂйШчЭМ2жаЃЌЕБABЃНAPЃЌЁЯBAPЃН90ЁуЃЌЩшжБЯпl2НЛxжсгкNЃЎЩшOBЃНmЃЌдђOAЃН2mЃЌРэгЩШЋЕШШ§НЧаЮЕФаджЪЃЌЙЙНЈЗНГЬНтОіЮЪЬтЃЎЂкШчЭМ3жаЃЌЕБABЃНAPЁфЃЌЁЯBAPЁфЃН90ЁуЪБЃЌЩшOBЃНmЃЌOAЃН2mЃЌРэгЩШЋЕШШ§НЧаЮЕФаджЪЙЙНЈЗНГЬНтОіЮЪЬтЃЎЂлШчЭМ3жаЃЌЕБABЃНPBЃЌЁЯABPЃН90ЁуЪБЃЌЭЌЗЈПЩЕУ.
НтЃКЃЈ1ЃЉЖдгкжБЯпyЃН![]() x+bЃЌСюxЃН0ЃЌЕУЕНyЃНbЃЌСюyЃН0ЃЌЕУЕНxЃНЉ2bЃЌ
x+bЃЌСюxЃН0ЃЌЕУЕНyЃНbЃЌСюyЃН0ЃЌЕУЕНxЃНЉ2bЃЌ
ЁрAЃЈЉ2bЃЌ0ЃЉЃЌBЃЈ0ЃЌbЃЉ
ЙЪД№АИЮЊЃЈЉ2bЃЌ0ЃЉЃЌЃЈ0ЃЌbЃЉЃЛ
ЃЈ2ЃЉЁїABCЪЧЕШбќжБНЧШ§НЧаЮЃЎ
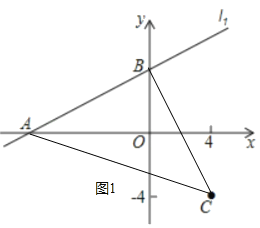
РэгЩЃКЁпbЃН4ЃЌ
ЁрAЃЈЉ8ЃЌ0ЃЉЃЌBЃЈ0ЃЌ4ЃЉЃЌЁпCЃЈ4ЃЌЉ4ЃЉЃЌ
ЁрABЃН![]() ЃЌ
ЃЌ
ЁрABЃНBCЃЌ
ЁпAB2+BC2ЃНЃЈ4![]() ЃЉ2+ЃЈ4
ЃЉ2+ЃЈ4![]() ЃЉ2ЃН160ЃЌAC2ЃН160ЃЌ
ЃЉ2ЃН160ЃЌAC2ЃН160ЃЌ
ЁрAB2+BC2ЃНAC2ЃЌ
ЁрЁЯABCЃН90ЁуЃЌ
ЁрЁїABCЪЧЕШбќжБНЧШ§НЧаЮЃЛ
ЃЈ3ЃЉЂйШчЭМ2жаЃЌЕБABЃНAPЃЌЁЯBAPЃН90ЁуЃЌЩшжБЯпl2НЛxжсгкNЃЎ
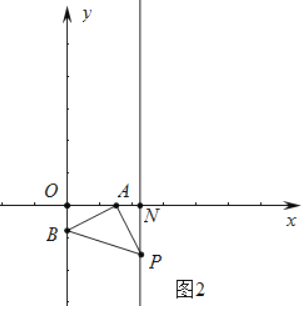
ЁпOAЃН2OBЃЌЩшOBЃНmЃЌдђOAЃН2mЃЌ
гЩЁїAOBЁеЁїPNAЃЌПЩЕУANЃНOBЃНmЃЌPNЃНOAЃН2mЃЌ
ЁрONЃН3mЃН4ЃЌ
ЁрmЃН![]() ЃЌ
ЃЌ
ЁрPMЃН![]() ЃЌ
ЃЌ
ЁрPЃЈ4ЃЌЉ![]() ЃЉЃЎ
ЃЉЃЎ
ЂкШчЭМ3жаЃЌЕБABЃНAPЁфЃЌЁЯBAPЁфЃН90ЁуЪБЃЌЩшOBЃНmЃЌOAЃН2mЃЌ
гЩЁїAOBЁеЁїPЁфNAЃЌПЩЕУANЃНOBЃНmЃЌPЁфNЃНOAЃН2mЃЌ
ЁпONЃН4ЃН2mЉmЃЌ
ЁрmЃН4ЃЌ
ЁрPЁфNЃН8ЃЌ
ЁрPЁфЃЈ4ЃЌ8ЃЉЃЌ
ЂлШчЭМ3жаЃЌЕБABЃНPBЃЌЁЯABPЃН90ЁуЪБЃЌЭЌЗЈПЩЕУPЃЈ4ЃЌЉ12ЃЉЃЎ
злЩЯЫљЪіЃЌТњзуЬѕМўЕФЕуPзјБъЮЊЃЈ4ЃЌЉ![]() ЃЉЛђЃЈ4ЃЌ8ЃЉЛђЃЈ4ЃЌЉ12ЃЉЃЎ
ЃЉЛђЃЈ4ЃЌ8ЃЉЛђЃЈ4ЃЌЉ12ЃЉЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЫљЪОЃЌдкЪ§жсЩЯЕуAБэЪОЕФгаРэЪ§ЮЊ-6ЃЌЕуBБэЪОЕФгаРэЪ§ЮЊ4ЃЌЕуPДгЕуAГіЗЂЃЌвдУПУы2ИіЕЅЮЛГЄЖШЕФЫйЖШдкЪ§жсЩЯЯђЕуBдЫЖЏЃЌЕБЕуPЕНДяЕуBКѓСЂМДЗЕЛиЃЌШдШЛвдУПУы2ИіЕЅЮЛГЄЖШЕФЫйЖШдЫЖЏжСЕуAЭЃжЙЃЎЩшдЫЖЏЪБМфЮЊtЃЈЕЅЮЛЃКУыЃЉЃЎ
ЃЈ1ЃЉЧѓt=1ЪБЕуPБэЪОЕФгаРэЪ§ЃЛ
ЃЈ2ЃЉЧѓЕуPгыЕуBжиКЯЪБЕФtжЕЃЛ
ЃЈ3ЃЉдкЕуPбиЪ§жсгЩЕуAЕНЕуBдйЛиЕНЕуAЕФдЫЖЏЙ§ГЬжаЃЌЧѓЕуPгыЕуAЕФОрРыЃЈгУКЌtЕФДњЪ§ЪНБэЪОЃЉЃЛ
ЃЈ4ЃЉЕБЕуPБэЪОЕФгаРэЪ§гыдЕуЕФОрРыЪЧ2ИіЕЅЮЛГЄЖШЪБЃЌжБНгаДГіЫљгаТњзуЬѕМўЕФtжЕ.
![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЂйНЋЯТСаИїЪ§ЬюШыЯргІЕФРЈКХжа:
0,-2019ЃЌ7.01,+6,+30Љ,![]()
ИКЪ§:{ }
е§Ъ§:{ }
ећЪ§:{ }
Ђк.ЛвЛЬѕЪ§жсЃЌдкЪ§жсЩЯБъГівдЯТИїЕуЃЌШЛКѓгУЁАЃМЁБЗћКХСЌЦ№РД.
-![]() ЃЛ-ЃЈ-4ЃЉЃЛ-|-1|ЃЛ
ЃЛ-ЃЈ-4ЃЉЃЛ-|-1|ЃЛ![]() ЃЛ0ЃЛ
ЃЛ0ЃЛ![]() ЃЛ2.5ЃЛ
ЃЛ2.5ЃЛ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПгУе§ЗНаЮгВжНАхзіШ§РтжљКазгЃЌУПИіКазггЩ3ИіОиаЮВрУцКЭ2Иіе§Ш§НЧаЮЕзУцзщГЩЁЃгВжНАхвдШчЭМСНжжЗНЪНВУМєЃЈВУМєКѓБпНЧСЯВЛдйРћгУЃЉ
AЗНЗЈЃКМє6ИіВрУцЃЛ BЗНЗЈЃКМє4ИіВрУцКЭ5ИіЕзУцЁЃ

Яжга19еХгВжНАхЃЌВУМєЪБ![]() еХгУAЗНЗЈЃЌЦфгргУBЗНЗЈЁЃ
еХгУAЗНЗЈЃЌЦфгргУBЗНЗЈЁЃ
ЃЈ1ЃЉгУ![]() ЕФДњЪ§ЪНЗжБ№БэЪОВУМєГіЕФВрУцКЭЕзУцЕФИіЪ§ЃЛ
ЕФДњЪ§ЪНЗжБ№БэЪОВУМєГіЕФВрУцКЭЕзУцЕФИіЪ§ЃЛ
ЃЈ2ЃЉШєВУМєГіЕФВрУцКЭЕзУцЧЁКУШЋВПгУЭъЃЌЮЪФмзіЖрЩйИіКазгЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПгавЛУцЛ§ЮЊ5![]() ЕФЕШбќШ§НЧаЮЃЌЫќЕФвЛИіФкНЧЪЧ30ЁуЃЌдђвдЫќЕФбќГЄЮЊБпЕФе§ЗНаЮЕФУцЛ§ЮЊ ЃЎ
ЕФЕШбќШ§НЧаЮЃЌЫќЕФвЛИіФкНЧЪЧ30ЁуЃЌдђвдЫќЕФбќГЄЮЊБпЕФе§ЗНаЮЕФУцЛ§ЮЊ ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЫљЪОЃЌдкЯТСаЬѕМўжаЃЌВЛФмзїЮЊХаЖЯЁїABDЁеЁїBACЕФЬѕМўЪЧЃЈ )

A. ЁЯDЃНЁЯCЃЌЁЯBADЃНЁЯABC B. ЁЯBADЃНЁЯABCЃЌЁЯABDЃНЁЯBAC
C. BDЃНACЃЌЁЯBADЃНЁЯABC D. ADЃНBCЃЌBDЃНAC
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃЌШчЭМЃЌABЁЮCDЃЌжБЯпEFЗжБ№НЛABЁЂCDгкЕуEЁЂFЃЌEGЦНЗжЁЯAEFЃЌFHЦНЗжЁЯEFDЃЎЧѓжЄЃКEGЁЮFHЃЎ

ЧыЭъГЩвдЯТжЄУїЙ§ГЬЃК
жЄУїЃКЁпABЁЮCD(вбжЊ)
ЁрЁЯAEF=ЁЯEFDЃЈ__________________ЃЉ
ЁпEGЦНЗжЁЯAEFЃЌFHЦНЗжЁЯEFDЃЈ__________ЃЉ
ЁрЁЯ___ЃН![]() ЁЯAEF,ЁЯ___=
ЁЯAEF,ЁЯ___= ![]() ЁЯEFDЃЈ____________ЃЉ
ЁЯEFDЃЈ____________ЃЉ
ЁрЁЯ_____=ЁЯ______(ЕШСПДњЛЛ)
ЁрEGЁЮFHЃЈ__________________ЃЉЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЩЬГЁЯњЪлвЛжжбЇЩњгУМЦЫуЦїЃЌНјМлЮЊУПЬЈ20дЊЃЌЪлМлЮЊУПЬЈ30дЊЪБЃЌУПжмПЩТє160ЬЈЃЌШчЙћУПЬЈЪлМлУПЩЯеЧ2дЊЃЌУПжмОЭЛсЩйТє20ЬЈЃЌЕЋГЇМвЙцЖЈзюИпУПЬЈЪлМлВЛФмГЌЙ§33дЊЃЌЕБМЦЫуЦїЖЈМлЮЊЖрЩйдЊЪБЃЌЩЬГЁУПжмЕФРћШѓЧЁКУЮЊ1680дЊЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
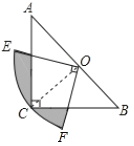
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌЁЯC=90ЁуЃЌAC=BCЃЌаББпAB=2ЃЌOЪЧABЕФжаЕуЃЌвдOЮЊдВаФЃЌЯпЖЮOCЕФГЄЮЊАыОЖЛдВаФНЧЮЊ90ЁуЕФЩШаЮOEFЃЌЛЁEFОЙ§ЕуCЃЌдђЭМжавѕгАВПЗжЕФУцЛ§ЮЊ________.
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com