
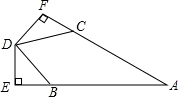
已知,如图,AB=AC,BD=CD,DE⊥AB于点E,DF⊥AC于点F,
(1)求证:DE=DF.
(2)连接BC,求证:线段AD垂直平分线段BC.
【考点】全等三角形的判定与性质;线段垂直平分线的性质.
【专题】证明题.
【分析】(1)连接AD,易证△ACD≌△ABD,根据全等三角形对应角相等的性质可得∠EAD=∠FAD,根据角平分线的性质,即可解答;
(2)由△ACD≌△ABD(已证),得到DC=DB,所以点D在线段BC的垂直平分线上.又AB=AC,所以点A在线段BC的垂直平分线上,即可解答.
【解答】解:(1)如图,连接AD.
在△ACD和△ABD中,
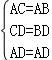
∴△ACD≌△ABD(SSS).
∴∠FAD=∠EAD,
即AD平分∠EAF.
又∵DE⊥AE,DF⊥AF,
∴DE=DF.
(2)∵△ACD≌△ABD(已证).
∴DC=DB,
∴点D在线段BC的垂直平分线上.
又∵AB=AC
∴点A在线段BC的垂直平分线上.
∵两点确定一条直线,
∴AD垂直平分BC.
【点评】本题考查了全等三角形的性质与判定,角平分线的性质、垂直平分线的性质,解决本题的关键是证明△ACD≌△ABD.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:初中数学 来源: 题型:
如图,已知在△ABC中,PR⊥AB于R,PS⊥AC于S,PR=PS,∠1=∠2,则四个结论:①AR=AS;②PQ∥AB;③△BPR≌△CPS;④BP=CP中( )
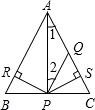
A.全部正确 B.仅①②正确 C.仅①正确 D.仅①④正确
查看答案和解析>>
科目:初中数学 来源: 题型:
下列说法中正确的个数是( )
(1)﹣a表示负数;
(2)多项式﹣3a2b+7a2b2﹣2ab+l的次数是3;
(3)单项式﹣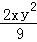 的系数为﹣2;
的系数为﹣2;
(4)若|x|=﹣x,则x<0.
A.0个 B.1个 C.2个 D.3个
查看答案和解析>>
科目:初中数学 来源: 题型:
把下列各数按要求填入相应的大括号里:
5,﹣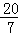 ,0,﹣(﹣3),2.10010001…,42,﹣2π,﹣10,
,0,﹣(﹣3),2.10010001…,42,﹣2π,﹣10,
整数集合:{ …},
分数集合:{ …},
正有理数集合:{ …},
无理数集合:{ …}.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com