
【题目】已知:在平面直角坐标系中,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,
,![]() (点
(点![]() 在点
在点![]() 的右侧),点
的右侧),点![]() 为抛物线的顶点,点
为抛物线的顶点,点![]() 的纵坐标为-2.
的纵坐标为-2.
(1)如图1,求此抛物线的解析式;
(2)如图2,点![]() 是第一象限抛物线上一点,连接
是第一象限抛物线上一点,连接![]() ,过点
,过点![]() 作
作![]() 轴交
轴交![]() 于点
于点![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() ,
,![]() 的长为
的长为![]() ,求
,求![]() 与
与![]() 的函数关系式(不要求写出自变量
的函数关系式(不要求写出自变量![]() 的取值范围);
的取值范围);
(3)如图3,在(2)的条件下,点![]() 在
在![]() 上,且
上,且![]() ,点
,点![]() 的横坐标大于3,连接
的横坐标大于3,连接![]() ,
,![]() ,
,![]() ,且
,且![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,若
,若![]() ,求点
,求点![]() 的坐标.
的坐标.

【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)将抛物线解析式化为顶点式可得y=a(x-1)2-4a,则C点为(1,-4a),再由-4a=-2即可求a的值,进而确定函数解析式;
(2)由已知分别求出点P和点A的坐标,可得AP的直线解析式,求出D点坐标则可求CD;
(3)设CD与x轴的交点为H,连接BE,由三角形中位线的性质可求BE=2(t-3)=2t-6;过点F作FN⊥BE于点N,过点P作PM⊥BE交BE的延长线于点M,可证明Rt△PME≌Rt△ENF(HL),从而推导出∠EPF=∠EFP=45°;过点C作CK⊥CG交PA的延长线于点K,连接AC、BC,能够进一步证明△ACK≌△BCG(SAS),得到∠KGB=90°;令AG=8m,则CG=![]() BG=6m,过点G作GL⊥x轴于点L,在Rt△ABG中,AG=10m=4,求出m值,利用等积法可求G点的坐标,再将G点坐标代入
BG=6m,过点G作GL⊥x轴于点L,在Rt△ABG中,AG=10m=4,求出m值,利用等积法可求G点的坐标,再将G点坐标代入![]() ,求出t,即可求出点P坐标.
,求出t,即可求出点P坐标.
解:(1)![]() ,
,
![]() 顶点
顶点![]() 的坐标为
的坐标为![]() ,
,
![]() 点
点![]() 的纵坐标为
的纵坐标为![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
(2)![]() 点
点![]() 的横坐标为
的横坐标为![]() ,
,
![]() ,
,
![]() 与
与![]() 轴的交点为
轴的交点为![]() ,
,![]() ,
,
![]() 设
设![]() 的直线解析式为
的直线解析式为![]() ,
,
则有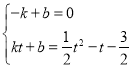 ,
,
解得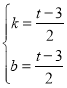 ,
,
![]() ,
,
![]() 轴交
轴交![]() 于点
于点![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
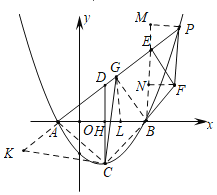
(3)如图:设![]() 与
与![]() 轴的交点为
轴的交点为![]() ,连接
,连接![]() ,
,
![]() 垂直平分
垂直平分![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() 轴,
轴,
![]() ,
,
过点![]() 作
作![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() 、
、![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
令![]() ,则
,则![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
过点![]() 作
作![]() 轴于点
轴于点![]() ,
,
在![]() 中,
中,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() 的解析式为
的解析式为![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]() ,
,![]() .
.


科目:初中数学 来源: 题型:
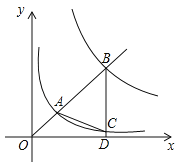
【题目】(2017浙江省湖州市,第16题,4分)如图,在平面直角坐标系xOy中,已知直线y=kx(k>0)分别交反比例函数![]() 和
和![]() 在第一象限的图象于点A,B,过点B作 BD⊥x轴于点D,交
在第一象限的图象于点A,B,过点B作 BD⊥x轴于点D,交![]() 的图象于点C,连结AC.若△ABC是等腰三角形,则k的值是______.
的图象于点C,连结AC.若△ABC是等腰三角形,则k的值是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
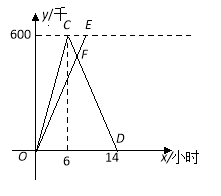
【题目】A,B两城相距600千米,甲、乙两车同时从A城出发驶向B城,甲车到达B城后立即返回.如图是它们离A城的距离y(千米)与行驶时间 x(小时)之间的函数图象.
(1)求甲车行驶过程中y与x之间的函数解析式,并写出自变量x的取值范围;
(2)当它们行驶了7小时时,两车相遇,求乙车的速度及乙车行驶过程中y与x之间的函数解析式,并写出自变量x的取值范围;
(3)当两车相距100千米时,求甲车行驶的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:在直角![]() 中,
中,![]() ,点
,点![]() 在边
在边![]() 上,且
上,且![]() 如果将
如果将![]() 沿
沿![]() 所在的直线翻折,点
所在的直线翻折,点![]() 恰好落在边
恰好落在边![]() 上的点
上的点![]() 处,点
处,点![]() 为
为![]() 边上的一个动点,联结
边上的一个动点,联结![]() ,以
,以![]() 圆心,
圆心,![]() 为半径作⊙
为半径作⊙![]() ,交线段
,交线段![]() 于点
于点![]() 和点
和点![]() ,作
,作![]() 交⊙
交⊙![]() 于点
于点![]() ,
,![]() 交线段
交线段![]() 于点
于点![]() .
.
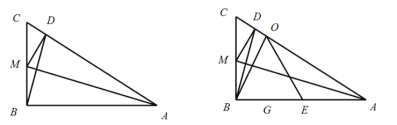
(1)求点![]() 到点
到点![]() 和直线
和直线![]() 的距离
的距离
(2)如果点![]() 平分劣弧
平分劣弧![]() ,求此时线段
,求此时线段![]() 的长度
的长度
(3)如果![]() 为等腰三角形,以
为等腰三角形,以![]() 为圆心的⊙
为圆心的⊙![]() 与此时的⊙
与此时的⊙![]() 相切,求⊙
相切,求⊙![]() 的半径
的半径
查看答案和解析>>
科目:初中数学 来源: 题型:
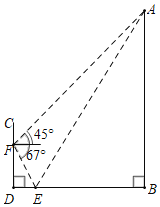
【题目】为了测量竖直旗杆AB的高度,某综合实践小组在地面D处竖直放置标杆CD,并在地面上水平放置一个平面镜E,使得B,E,D在同一水平线上(如图所示).该小组在标杆的F处通过平面镜E恰好观测到旗杆顶A(此时∠AEB=∠FED),在F处测得旗杆顶A的仰角为45°,平面镜E的俯角为67°,测得FD=2.4米.求旗杆AB的高度约为多少米?(结果保留整数,参考数据:sin67°≈![]() ,cos67°≈
,cos67°≈![]() ,tan67°≈
,tan67°≈![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
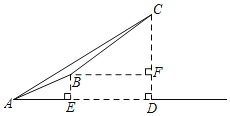
【题目】金佛山是巴蜀四大名山之一游客上金佛山有两种方式:一种是从西坡上山,如图,先从A沿登山步道走到点B,再沿索道乘坐缆车到点C;另一种是从北坡景区沿着盘山公路开车上山到点C.已知在点A处观测点C,得仰角∠CAD=37°,且A、B的水平距离AE=1000米,索道BC的坡度i=1:![]() ,长度为2600米,CD⊥AD于点D,BF⊥CD于点F则BE的高度为(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°=0.75,
,长度为2600米,CD⊥AD于点D,BF⊥CD于点F则BE的高度为(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°=0.75,![]() =1.73)( )
=1.73)( )
A.2436.8米B.2249.6米C.1036.8米D.1136.8米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 经过点
经过点![]() 和
和![]() .下列结论:①
.下列结论:①![]() ;②
;②![]() ;③当
;③当![]() 时,抛物线与
时,抛物线与![]() 轴必有一个交点在点
轴必有一个交点在点![]() 的右侧;④抛物线的对称轴为
的右侧;④抛物线的对称轴为![]() .
.
其中结论正确的个数有( )
A.4个B.3个C.2个D.1个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com