
【题目】金佛山是巴蜀四大名山之一游客上金佛山有两种方式:一种是从西坡上山,如图,先从A沿登山步道走到点B,再沿索道乘坐缆车到点C;另一种是从北坡景区沿着盘山公路开车上山到点C.已知在点A处观测点C,得仰角∠CAD=37°,且A、B的水平距离AE=1000米,索道BC的坡度i=1:![]() ,长度为2600米,CD⊥AD于点D,BF⊥CD于点F则BE的高度为(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°=0.75,
,长度为2600米,CD⊥AD于点D,BF⊥CD于点F则BE的高度为(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°=0.75,![]() =1.73)( )
=1.73)( )
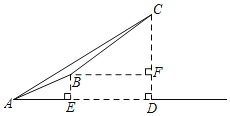
A.2436.8米B.2249.6米C.1036.8米D.1136.8米
【答案】D
【解析】
在Rt△BCF中,根据BC的坡度i=1:![]() ,求得∠CBF=30°,根据三角函数的定义得到CF=1300,BF=1300
,求得∠CBF=30°,根据三角函数的定义得到CF=1300,BF=1300![]() ,根据矩形的性质得到DE=BF=1300
,根据矩形的性质得到DE=BF=1300![]() ,根据三角函数的定义即可得到结论.
,根据三角函数的定义即可得到结论.
解:在Rt△BCF中,∵BC的坡度i=1:![]() ,
,
∴∠CBF=30°,
∵BC=2600,
∴CF=1300,BF=1300![]() ,
,
∵CD⊥AD于点D,BF⊥CD,BE⊥AD,
∴四边形BEDF是矩形,
∴DE=BF=1300![]() ,
,
∵AE=1000米,
∴AD=AE+DE=1000+1300![]() ,
,
∵∠CAD=37°,
∴CD=ADtan37°=(1000+1300![]() )×0.75=2436.75,
)×0.75=2436.75,
∴BE=DF=2436.75﹣1300≈1136.8米,
答:BE的高度为1136.8米.
故选:D.


科目:初中数学 来源: 题型:
【题目】已知:![]() 内接于
内接于![]() ,过点
,过点![]() 作
作![]() 的切线,交
的切线,交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() .
.
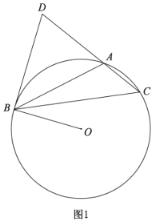

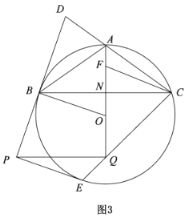
(1)如图1,求证:![]() ;
;
(2)如图2,过点![]() 作
作![]() 于点
于点![]() ,连接
,连接![]() ,交
,交![]() 于点
于点![]() ,
,![]() ,求证:
,求证:![]() ;
;
(3)如图3,在(2)的条件下,点![]() 为
为![]() 上一点,过点
上一点,过点![]() 的切线交
的切线交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() ,
,![]() ,点
,点![]() 为
为![]() 上一点,连接
上一点,连接![]() ,若
,若![]() ,
,![]() ,
,![]() ,
,![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如右图,点A的坐标为(0,1),点B是x轴正半轴上的一动点,以AB为边作等腰直角△ABC,使∠BAC=90°,如果点B的横坐标为x,点C的纵坐标为y,那么表示y与x的函数关系的图像大致是( )
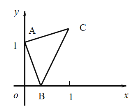
A.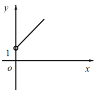 B.
B.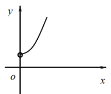
C.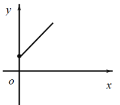 D.
D.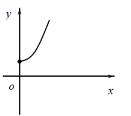
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在平面直角坐标系中,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,
,![]() (点
(点![]() 在点
在点![]() 的右侧),点
的右侧),点![]() 为抛物线的顶点,点
为抛物线的顶点,点![]() 的纵坐标为-2.
的纵坐标为-2.
(1)如图1,求此抛物线的解析式;
(2)如图2,点![]() 是第一象限抛物线上一点,连接
是第一象限抛物线上一点,连接![]() ,过点
,过点![]() 作
作![]() 轴交
轴交![]() 于点
于点![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() ,
,![]() 的长为
的长为![]() ,求
,求![]() 与
与![]() 的函数关系式(不要求写出自变量
的函数关系式(不要求写出自变量![]() 的取值范围);
的取值范围);
(3)如图3,在(2)的条件下,点![]() 在
在![]() 上,且
上,且![]() ,点
,点![]() 的横坐标大于3,连接
的横坐标大于3,连接![]() ,
,![]() ,
,![]() ,且
,且![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,若
,若![]() ,求点
,求点![]() 的坐标.
的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,AB=AC,AD是BC边上的中线,点E是AD上一点,过点B作BF∥EC,交AD的延长线于点F,连接BE,CF.
(1)求证:△BDF≌△CDE;
(2)当ED与BC满足什么数量关系时,四边形BECF是正方形?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人驾车分别从A、B两地相向而行,乙出发半小时后甲出发,甲出发1.5小时后汽车出现故障,于是甲停下修车,半小时后甲修好后继续沿原路按原速与乙相遇,相遇后甲随即调头以原速返回A地,乙也继续向A地行驶,甲、乙两车之间的距离(y/千米)与甲驾车时间x(小时)之间的关系如图所示,当乙到达A地时,甲距离B地_____千米.
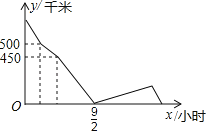
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,已知抛物线y=﹣![]() x2+
x2+![]() x+2
x+2![]() 与x轴交于A、B两点,与y轴交于C点,抛物线的顶点为Q,连接BC.
与x轴交于A、B两点,与y轴交于C点,抛物线的顶点为Q,连接BC.
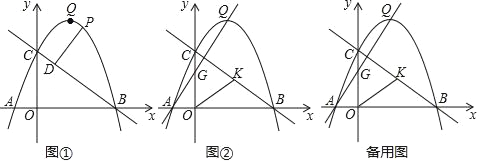
(1)求直线BC的解析式;
(2)点P是直线BC上方抛物线上的一点,过点P作PD⊥BC于点D,在直线BC上有一动点M,当线段PD最大时,求PM+![]() MB最小值;
MB最小值;
(3)如图②,直线AQ交y轴于G,取线段BC的中点K,连接OK,将△GOK沿直线AQ平移得△G′O'K′,将抛物线y=﹣![]() x2+
x2+![]() x+2
x+2![]() 沿直线AQ平移,记平移后的抛物线为y′,当抛物线y′经过点Q时,记顶点为Q′,是否存在以G'、K'、Q'为顶点的三角形是等腰三角形?若存在,求出点G′的坐标;若不存在,请说明理由.
沿直线AQ平移,记平移后的抛物线为y′,当抛物线y′经过点Q时,记顶点为Q′,是否存在以G'、K'、Q'为顶点的三角形是等腰三角形?若存在,求出点G′的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知点A(-2,0),B(2,0),点P在直线![]() 上,若△ABP是直角三角形,则点P的坐标为______________.
上,若△ABP是直角三角形,则点P的坐标为______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,直线y=﹣![]() x+2与x轴交于点B,与y轴交于点C,抛物线y=-
x+2与x轴交于点B,与y轴交于点C,抛物线y=-![]() x2+bx+c经过B、C两点,点P是抛物线上的一个动点,过点P作PQ⊥x轴,垂足为Q,交直线y=﹣
x2+bx+c经过B、C两点,点P是抛物线上的一个动点,过点P作PQ⊥x轴,垂足为Q,交直线y=﹣![]() x+2于点D.设点P的横坐标为m.
x+2于点D.设点P的横坐标为m.
(1)求该抛物线的函数表达式;
(2)若以P、D、O、C为顶点的四边形是平行四边形,求点Q的坐标;
(3)如图2,当点P位于直线BC上方的抛物线上时,过点P作PE⊥BC于点E,求当PE取得最大值时点P的坐标,并求PE的最大值.
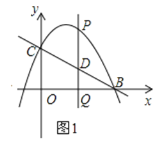
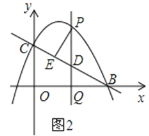
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com