
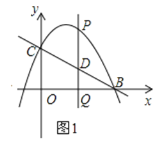
����Ŀ����ͼ1��ֱ��y����![]() x+2��x�ύ�ڵ�B����y�ύ�ڵ�C��������y��-
x+2��x�ύ�ڵ�B����y�ύ�ڵ�C��������y��-![]() x2+bx+c����B��C���㣬��P���������ϵ�һ�����㣬����P��PQ��x�ᣬ����ΪQ����ֱ��y����
x2+bx+c����B��C���㣬��P���������ϵ�һ�����㣬����P��PQ��x�ᣬ����ΪQ����ֱ��y����![]() x+2�ڵ�D�����P�ĺ�����Ϊm��
x+2�ڵ�D�����P�ĺ�����Ϊm��
��1����������ߵĺ�������ʽ��
��2������P��D��O��CΪ������ı�����ƽ���ı��Σ����Q�����ꣻ
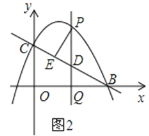
��3����ͼ2������Pλ��ֱ��BC�Ϸ�����������ʱ������P��PE��BC�ڵ�E����PEȡ�����ֵʱ��P�����꣬����PE�����ֵ��
���𰸡���1��y����![]() x2+
x2+![]() x+2����2��(2��0)��(2+2
x+2����2��(2��0)��(2+2![]() ��0)��(2��2
��0)��(2��2![]() ��0)����3��P(2��3)��PE���ֵΪ
��0)����3��P(2��3)��PE���ֵΪ![]() ��
��
��������
��1������ֱ��y����![]() x+2��x�ύ�ڵ�B����y�ύ�ڵ�C�����B��C�������꣬����y��-
x+2��x�ύ�ڵ�B����y�ύ�ڵ�C�����B��C�������꣬����y��-![]() x2+bx+c�ɵù���b��c�Ķ�Ԫһ�η����飬�ⷽ�������b��c��ֵ���ɵô𰸣�
x2+bx+c�ɵù���b��c�Ķ�Ԫһ�η����飬�ⷽ�������b��c��ֵ���ɵô𰸣�
��2������PQ��x�ᣬֱ��y����![]() x+2�ڵ�D����P�ĺ�����Ϊm����m��ʾ��D��Q�������꣬����ƽ���ı��ε����ʿɵ�OC=PD=2�������������빫ʽ���m��ֵ���ɵô𰸣�
x+2�ڵ�D����P�ĺ�����Ϊm����m��ʾ��D��Q�������꣬����ƽ���ı��ε����ʿɵ�OC=PD=2�������������빫ʽ���m��ֵ���ɵô𰸣�
��3�����ù��ɶ��������BC�ij�������ƽ���ߵ����ʿɵá�OCB����PDE����֤����PED�ס�BOC���������������ε����ʿ���m��ʾ��PE�ij������ݶ��κ��������ʼ��ɵô𰸣�
��1����ֱ��y����![]() x+2��x�ύ�ڵ�B����y�ύ�ڵ�C��
x+2��x�ύ�ڵ�B����y�ύ�ڵ�C��
���B��C������ֱ�Ϊ��4��0������0��2����
��������y��-![]() x2+bx+c����B��C���㣬
x2+bx+c����B��C���㣬
��![]() ��
��
���![]() ��
��
����κ�������ʽΪy����![]() x2+
x2+![]() x+2��
x+2��
��2����P�����������ϣ�������Ϊm��
��P��������m����![]() m2+
m2+![]() m+2����
m+2����
��PQ��x�ᣬ����ΪQ����ֱ��y����![]() x+2�ڵ�D��
x+2�ڵ�D��
��Q������m��0����D��������m����![]() m+2����
m+2����
��P��D��O��CΪ������ı���Ϊƽ���ı���ʱ������PD��OC��2��
��|��![]() m2+
m2+![]() m+2������
m+2������![]() m+2��|��2����|��
m+2��|��2����|��![]() m2+2m|��2��
m2+2m|��2��
����![]() m2+2m��2ʱ��
m2+2m��2ʱ��
��ã�m��2��
��Q������2��0����
����![]() m2+2m����2ʱ��
m2+2m����2ʱ��
��ã�m��2��2![]() ��
��
��Q������2+2![]() ��0����2��2
��0����2��2![]() ��0����
��0����
���Ͽ�֪��Q������Ϊ��2��0����2+2![]() ��0����2��2
��0����2��2![]() ��0����
��0����
��3���ɣ�2����֪P������Ϊ��m����![]() m2+
m2+![]() m+2����Q������m��0����D��������m����
m+2����Q������m��0����D��������m����![]() m+2����
m+2����
��PD����![]() m2+2m��
m2+2m��
��Rt��OBC��OC��2��OB��4��
��BC��![]() =2
=2![]() ��
��
��PQ��OC��
���OCB����PDE��
��PE��BC��
���PED����COB��90����
���PED�ס�BOC��
��![]() ��
��
��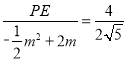 ��
��
���PE��![]() ��
��
��P��ֱ��BC�Ϸ���
��0��m��4��
�൱m��2ʱ PE�����ֵ![]() ��
��
��m��2ʱ����![]() m2+
m2+![]() m+2=3��
m+2=3��
���ʱP������Ϊ��2��3����


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ɽ�ǰ����Ĵ���ɽ֮һ�ο��Ͻ��ɽ�����ַ�ʽ��һ���Ǵ�������ɽ����ͼ���ȴ�A�ص�ɽ�����ߵ���B���������������³�����C����һ���Ǵӱ��¾���������ɽ��·������ɽ����C����֪�ڵ�A���۲��C�������ǡ�CAD��37������A��B��ˮƽ����AE��1000�ף�����BC���¶�i��1��![]() ������Ϊ2600�ף�CD��AD�ڵ�D��BF��CD�ڵ�F��BE�ĸ߶�Ϊ���ο����ݣ�sin37���0.60��cos37���0.80��tan37����0.75��
������Ϊ2600�ף�CD��AD�ڵ�D��BF��CD�ڵ�F��BE�ĸ߶�Ϊ���ο����ݣ�sin37���0.60��cos37���0.80��tan37����0.75��![]() ��1.73����������
��1.73����������
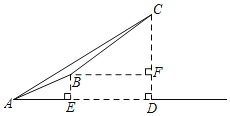
A.2436.8��B.2249.6��C.1036.8��D.1136.8��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() Ϊ�ȱ������Σ�
Ϊ�ȱ������Σ�![]() Ϊ�����ģ�����
Ϊ�����ģ�����![]() ��
��![]() �ڵ�
�ڵ�![]() �� ��
�� ��![]() ����
Ϊ����![]() ��һ���㣬������
��һ���㣬������![]() �Ƶ�
�Ƶ�![]() ��ʱ����ת
��ʱ����ת![]() ��������
��������![]() ���ڵ�
���ڵ�![]() ����
����![]() ʱ��
ʱ��![]() �ij���Ϊ__________
�ij���Ϊ__________

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������![]() ������
������![]() ��
��![]() �����н��ۣ���
�����н��ۣ���![]() ����
����![]() ���۵�
���۵�![]() ʱ����������
ʱ����������![]() �����һ�������ڵ�
�����һ�������ڵ�![]() ���Ҳࣻ�������ߵĶԳ���Ϊ
���Ҳࣻ�������ߵĶԳ���Ϊ![]() ��
��
���н�����ȷ�ĸ����У� ��
A.4��B.3��C.2��D.1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
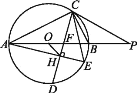
����Ŀ����ͼ,��ABC�ڽ��ڨ�O,AB�Ǩ�O��ֱ��,CDƽ�֡�ACB����O�ڵ�D,��AB�ڵ�F,��AE��CD�ڵ�H,����CE��OH.
(1)�ӳ�AB��Բ��һ��P,����PC,��PC2=PB��PA,��֤:PC�Ǩ�O������;
(2)��֤:CF��AE=AC��BC;
(3)��![]() =
=![]() ,��O�İ뾶��
,��O�İ뾶��![]() ,��tan��AEC��OH�ij�.
,��tan��AEC��OH�ij�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����0��������90������ô����sin����cos����tan����cot��Ϊ���ߵ���ABC������Բ�뾶�����Բ�뾶֮���ǣ� ��
A.2![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
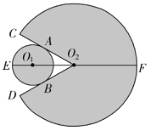
����Ŀ��ij�����һ��Բ�������һ������������ɣ���ͼ���ڡ�O1������O2CD�У���O1��O2C��O2D�ֱ����ڵ�A��B����֪��CO2D��60����E��F��ֱ��O1O2���O1������O2CD���������㣬��EF��24cm�����O1�İ뾶Ϊxcm��
��1���ú�x�Ĵ���ʽ��ʾ����O2CD�İ뾶��
��2������O1������O2CD��������������ɱ��ֱ�Ϊ0.45Ԫ/cm2��0.06Ԫ/cm2������O1�İ뾶Ϊ����ʱ������ߵ������ɱ���С��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() ����
����![]() ������ֱ��
������ֱ��![]() ����B��C���㣬��B������Ϊ
����B��C���㣬��B������Ϊ![]() ��
��
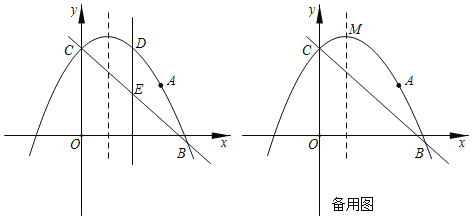
��1���������ߵĽ���ʽ��
��2����DΪ��������λ��ֱ��![]() �Ϸ���һ�㣬����D��
�Ϸ���һ�㣬����D��![]() �ύֱ��
�ύֱ��![]() �ڵ�E����PΪ�Գ�����һ���㣬���߶�
�ڵ�E����PΪ�Գ�����һ���㣬���߶�![]() �ij������ʱ����
�ij������ʱ����![]() ����Сֵ��
����Сֵ��
��3�����MΪ�����ߵĶ��㣬��y�����Ƿ���ڵ�Q��ʹ![]() �������ڣ����Q�����ꣻ�������ڣ���˵�����ɣ�
�������ڣ����Q�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˽�ijУ���꼶������Ŀѵ��������Ӱ��꼶ѧ���������ȡ�˲���ѧ��������һ��������Ŀ���ԣ��Ѳ��Խ����Ϊ�ĸ��ȼ���A�������㣻B�������ã�C��������D�����������������Խ�����������������������ͳ��ͼ![]() �����ͳ��ͼ�е���Ϣ����������⣺
�����ͳ��ͼ�е���Ϣ����������⣺

��1��ͼ1��![]() �Ķ�����__________������ͼ2����ͳ��ͼ����������
�Ķ�����__________������ͼ2����ͳ��ͼ����������
��2����ȡ���ⲿ�ֵ�ѧ����������Ŀ���Խ������λ������__________����
��3�����ν����㡢���á����������Ϊ90�֡�80�֡�70�֡�50�֣�������ȡ���ⲿ��ѧ��������ƽ���ɼ���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com