
【题目】如图,![]() 为等边三角形,
为等边三角形,![]() 为其内心,射线
为其内心,射线![]() 交
交![]() 于点
于点![]() , 点
, 点![]() 为射线
为射线![]() 上一动点,将射线
上一动点,将射线![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() ,与射线
,与射线![]() 交于点
交于点![]() ,当
,当![]() 时,
时,![]() 的长度为__________
的长度为__________

【答案】![]() 或
或![]() ;
;
【解析】
根据等边三角形的性质和内心的定义可得∠BAC=∠ABC=∠ACB=60°,AD平分∠BAC,AB=BC=AC,然后利用锐角三角函数求出BD、CD、OD和OC,然后根据点P和点O的相对位置分类讨论,分别画出对应的图形,利用全等三角形的判定及性质、锐角三角函数和相似三角形的判定及性质即可求出结论.
解:∵![]() 为等边三角形,
为等边三角形,![]() 为其内心,
为其内心,![]()
∴∠BAC=∠ABC=∠ACB=60°,AD平分∠BAC,AB=BC=AC
∴AD⊥BC,BD=CD,∠BAD=∠CAD=![]() ∠BAC=30°
∠BAC=30°
∴BD=CD=![]() =
=![]() ,AB =AC=BC=2BD=
,AB =AC=BC=2BD=![]()
连接OC
易知OC=OA,∠OCD=30°
在Rt△OCD中,OD=CD·tan∠OCD=2,OC=2OD=4
①当点P在点O上方时,如下图所示,设射线![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 后,点P的对应点为E,连接BE,过点E作EF⊥BC于F
后,点P的对应点为E,连接BE,过点E作EF⊥BC于F

∴∠PCE=60°,EC=PC,AP=AD-OD-PO=3
∴∠PCE=∠ACB=60°
∴∠ECB=∠PCA
∵BC=AC
∴△ECB≌△PCA
∴BE=AP=3,∠EBC=∠PAC=30°
∴EF=BE·sin∠EBC=![]() ,BF= BE·cos∠EBC=
,BF= BE·cos∠EBC=![]()
∴CF=BC-BF=![]()
∵EF⊥BC,AQ⊥BC
∴EF∥AQ
∴△CDQ∽△CFE
∴![]()
即
解得:DQ=![]() ;
;
②当点P在点O下方时,如下图所示,设射线![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 后,点P的对应点为E,连接BE,过点E作EF⊥BC于F
后,点P的对应点为E,连接BE,过点E作EF⊥BC于F

∴∠PCE=60°,EC=PC,AP=AD-OD+PO=5
∴∠PCE=∠ACB=60°
∴∠ECB=∠PCA
∵BC=AC
∴△ECB≌△PCA
∴BE=AP=5,∠EBC=∠PAC=30°
∴EF=BE·sin∠EBC=![]() ,BF= BE·cos∠EBC=
,BF= BE·cos∠EBC=![]()
∴CF=BC-BF=![]()
∵EF⊥BC,AQ⊥BC
∴EF∥AQ
∴△CDQ∽△CFE
∴![]()
即
解得:DQ=![]() ;
;
综上:DQ=![]() 或
或![]()
故答案为:![]() 或
或![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
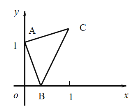
【题目】如右图,点A的坐标为(0,1),点B是x轴正半轴上的一动点,以AB为边作等腰直角△ABC,使∠BAC=90°,如果点B的横坐标为x,点C的纵坐标为y,那么表示y与x的函数关系的图像大致是( )
A.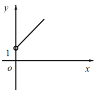 B.
B.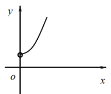
C.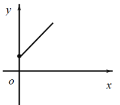 D.
D.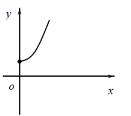
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,已知抛物线y=﹣![]() x2+
x2+![]() x+2
x+2![]() 与x轴交于A、B两点,与y轴交于C点,抛物线的顶点为Q,连接BC.
与x轴交于A、B两点,与y轴交于C点,抛物线的顶点为Q,连接BC.
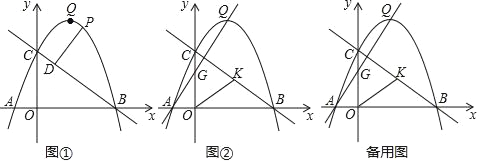
(1)求直线BC的解析式;
(2)点P是直线BC上方抛物线上的一点,过点P作PD⊥BC于点D,在直线BC上有一动点M,当线段PD最大时,求PM+![]() MB最小值;
MB最小值;
(3)如图②,直线AQ交y轴于G,取线段BC的中点K,连接OK,将△GOK沿直线AQ平移得△G′O'K′,将抛物线y=﹣![]() x2+
x2+![]() x+2
x+2![]() 沿直线AQ平移,记平移后的抛物线为y′,当抛物线y′经过点Q时,记顶点为Q′,是否存在以G'、K'、Q'为顶点的三角形是等腰三角形?若存在,求出点G′的坐标;若不存在,请说明理由.
沿直线AQ平移,记平移后的抛物线为y′,当抛物线y′经过点Q时,记顶点为Q′,是否存在以G'、K'、Q'为顶点的三角形是等腰三角形?若存在,求出点G′的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知点A(-2,0),B(2,0),点P在直线![]() 上,若△ABP是直角三角形,则点P的坐标为______________.
上,若△ABP是直角三角形,则点P的坐标为______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
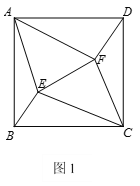
【题目】在四边形ABCD中,AB=AD,CB=CD,∠ABC=∠ADC=90°,∠BAD=α,∠BCD=β,点E,F是四边形ABCD内的两个点,满足∠EAF=![]() ,∠ECF=
,∠ECF=![]() ,连接BE,EF,FD.
,连接BE,EF,FD.
(1)如图1,当α=β时,判断∠ABE和∠ADF之间的数量关系,并证明你的猜想;
(2)当α≠β时,用等式表示线段BE,EF,FD之间的数量关系(直接写出即可)
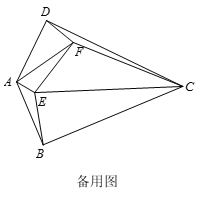
查看答案和解析>>
科目:初中数学 来源: 题型:
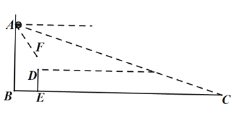
【题目】如图,在教室前面墙壁![]() 处安装了一个摄像头,当恰好观测到后面墙壁与底面交接处点
处安装了一个摄像头,当恰好观测到后面墙壁与底面交接处点![]() 时,摄像头俯角约为
时,摄像头俯角约为![]() ,受安装支架限制,摄像头观测的俯角最大约为
,受安装支架限制,摄像头观测的俯角最大约为![]() ,已知摄像头安装点高度
,已知摄像头安装点高度![]() 约为
约为![]() 米,摄像头与安装的墙壁之间距离忽略不计,
米,摄像头与安装的墙壁之间距离忽略不计,
![]() 求教室的长(教室前后墙壁之间的距离
求教室的长(教室前后墙壁之间的距离![]() 的值);
的值);
![]() 若第一排桌子前边缘与前面墙壁的距离
若第一排桌子前边缘与前面墙壁的距离![]() 为
为![]() 米, 桌子的高度
米, 桌子的高度![]() 为
为![]() 米,那么第一排桌子是否在监控范围内?如果不在,应该怎样移动? (
米,那么第一排桌子是否在监控范围内?如果不在,应该怎样移动? (![]() ,精确到
,精确到![]() 米)
米)
查看答案和解析>>
科目:初中数学 来源: 题型:
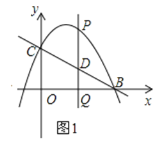
【题目】如图1,直线y=﹣![]() x+2与x轴交于点B,与y轴交于点C,抛物线y=-
x+2与x轴交于点B,与y轴交于点C,抛物线y=-![]() x2+bx+c经过B、C两点,点P是抛物线上的一个动点,过点P作PQ⊥x轴,垂足为Q,交直线y=﹣
x2+bx+c经过B、C两点,点P是抛物线上的一个动点,过点P作PQ⊥x轴,垂足为Q,交直线y=﹣![]() x+2于点D.设点P的横坐标为m.
x+2于点D.设点P的横坐标为m.
(1)求该抛物线的函数表达式;
(2)若以P、D、O、C为顶点的四边形是平行四边形,求点Q的坐标;
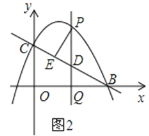
(3)如图2,当点P位于直线BC上方的抛物线上时,过点P作PE⊥BC于点E,求当PE取得最大值时点P的坐标,并求PE的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
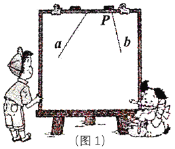
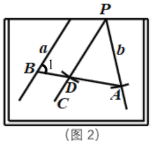
【题目】已知:如图1,直线![]() ,
,![]() 所成的角跑到画板外面去了,你有什么办法作出这两条直线所成角的角平分线?
所成的角跑到画板外面去了,你有什么办法作出这两条直线所成角的角平分线?
小明的做法是:
(1)如图2,画![]() ;
;
(2)以![]() 为圆心,任意长为半径画圆弧,分别交直线
为圆心,任意长为半径画圆弧,分别交直线![]() ,
,![]() 于点
于点![]() ,
,![]() ;
;
(3)连结![]() 并延长交直线
并延长交直线![]() 于点
于点![]() ;
;
请你先完成下面的证明,然后完成第(4)步作图:
∵![]()
∴![]() ( )
( )
∵以![]() 为圆心,任意长为半径画圆弧,分别交直线
为圆心,任意长为半径画圆弧,分别交直线![]() ,
,![]() 于点
于点![]() ,
,![]()
∴![]()
∴![]()
∴![]()
∴以直线![]() ,
,![]() 的交点和点
的交点和点![]() 、
、![]() 为顶点所构成的三角形为等腰三角形( )
为顶点所构成的三角形为等腰三角形( )
根据上面的推理证明完成第(4)步作图
(4)请在图2画板内作出“直线![]() ,
,![]() 所成的跑到画板外面去的角”的平分线(画板内的部分),尺规作出图形,并保留作图痕迹.
所成的跑到画板外面去的角”的平分线(画板内的部分),尺规作出图形,并保留作图痕迹.
第(4)步这么作图的理论依据是: .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com