
【题目】四边形![]() 是正方形,
是正方形,![]() 、
、![]() 分别是
分别是![]() 和
和![]() 的延长线上的点,且
的延长线上的点,且![]() ,连接
,连接![]() 、
、![]() 、
、![]() .
.
(1)求证:![]() ;
;
(2)若![]() ,
,![]() ,求
,求![]() 的面积.
的面积.

【答案】(1)证明见解析;(2)50
【解析】
(1)根据SAS证明![]() ,只要证明AD=AB,∠D=∠ABF,DE=BF即可;
,只要证明AD=AB,∠D=∠ABF,DE=BF即可;
(2)由于△ADE≌△ABF得∠BAF=∠DAE,则∠BAF+∠BAE=90°,即∠FAE=90°,根据旋转的定义可得到△ABF可以由△ADE绕旋转中心A点,按顺时针方向旋转90度得到;
先利用勾股定理可计算出AE=10,再根据△ABF可以由△ADE绕旋转中心A点,按顺时针方向旋转90度得到AE=AF,∠EAF=90°,然后根据直角三角形的面积公式计算即可.;
(1)∵四边形ABCD是正方形,
∴AD=AB,∠D=∠ABC=![]()
而F是CB的延长线上的点,
∴∠ABF=![]() ,
,
在△ADE和△ABF中

∴△ADE≌△ABF(SAS)
(2)∵△ADE≌△ABF
∴∠BAF=∠DAE,
而∠DAE+∠EAB=![]() ,
,
∴∠BAF+∠EAB=![]() ,即∠FAE=
,即∠FAE=![]() ,
,
∴△ABF可以由△ADE绕旋转中心A点,按顺时针方向旋转![]() 得到;
得到;
∵BC=8,
∴AD=8,
在Rt△ADE中,DE=6,AD=8,
∴AE=![]()
∵△ABF可以由△ADE绕旋转中心A点,按顺时针方向旋转![]() 得到,
得到,
∴AE=AF,∠EAF=![]() ,
,
∴△AEF的面积=![]()
故答案为:50


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
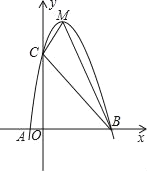
【题目】已知,如图,二次函数y=ax2+bx+c的图象与x轴交于A、B两点,其中A点坐标为(﹣1,0),点C(0,5),另抛物线经过点(1,8),M为它的顶点.
(1)求抛物线的解析式;
(2)求△MCB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,点
,点![]() 为底边
为底边![]() 上一动点,将射线
上一动点,将射线![]() 绕点
绕点![]() 逆时针旋转后,与射线
逆时针旋转后,与射线![]() 相交于点
相交于点![]() ,且
,且![]()
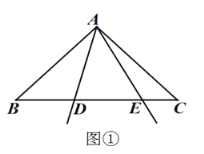
![]() 如图①,当点
如图①,当点![]() 在底边
在底边![]() 上,
上,![]() 时,请直接写出线段
时,请直接写出线段![]() 之间的数量关系;
之间的数量关系;
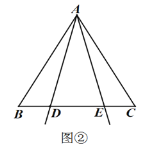
![]() 如图②,当点
如图②,当点![]() 在底边
在底边![]() 上,
上,![]() ,且
,且![]() 时,求证:
时,求证: ![]()
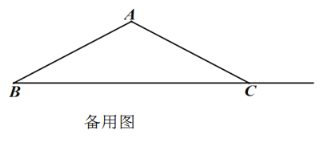
![]() 当
当![]() ,且
,且![]() 时,请直接写出
时,请直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 经过点
经过点![]() 和
和![]() .下列结论:①
.下列结论:①![]() ;②
;②![]() ;③当
;③当![]() 时,抛物线与
时,抛物线与![]() 轴必有一个交点在点
轴必有一个交点在点![]() 的右侧;④抛物线的对称轴为
的右侧;④抛物线的对称轴为![]() .
.
其中结论正确的个数有( )
A.4个B.3个C.2个D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
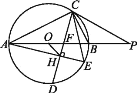
【题目】如图,△ABC内接于☉O,AB是☉O的直径,CD平分∠ACB交☉O于点D,交AB于点F,弦AE⊥CD于点H,连接CE、OH.
(1)延长AB到圆外一点P,连接PC,若PC2=PB·PA,求证:PC是☉O的切线;
(2)求证:CF·AE=AC·BC;
(3)若![]() =
=![]() ,☉O的半径是
,☉O的半径是![]() ,求tan∠AEC和OH的长.
,求tan∠AEC和OH的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
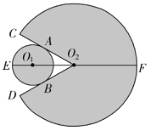
【题目】某玩具由一个圆形区域和一个扇形区域组成,如图,在⊙O1和扇形O2CD中,⊙O1与O2C、O2D分别切于点A、B,已知∠CO2D=60°,E、F是直线O1O2与⊙O1、扇形O2CD的两个交点,且EF=24cm,设⊙O1的半径为xcm,
(1)用含x的代数式表示扇形O2CD的半径;
(2)若⊙O1和扇形O2CD两个区域的制作成本分别为0.45元/cm2和0.06元/cm2,当⊙O1的半径为多少时,该玩具的制作成本最小?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是小章为学校举办的数学文化节没计的标志,在△ABC中,∠ACB=90°,以△ABC的各边为边作三个正方形,点G落在HI上,若AC+BC=6,空自部分面积为10.5,则阴影部分面积为______.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com