
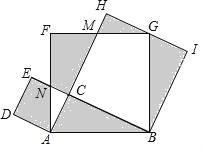
【题目】如图是小章为学校举办的数学文化节没计的标志,在△ABC中,∠ACB=90°,以△ABC的各边为边作三个正方形,点G落在HI上,若AC+BC=6,空自部分面积为10.5,则阴影部分面积为______.

【答案】17
【解析】
根据余角的性质得到∠FAC=∠ABC,根据全等三角形的性质得到S△FAM=S△ABN,推出S△ABC=S四边形FNCM,根据勾股定理得到AC2+BC2=AB2,解方程组得到3AB2=57,于是得到结论.
解:如图∵四边形ABGF是正方形,
∴∠FAB=∠AFG=∠ACB=90°,
∴∠FAC+∠BAC=∠FAC+∠ABC=90°,
∴∠FAC=∠ABC,
在△FAM与△ABN中,
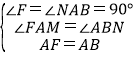 ,
,
∴△FAM≌△ABN(AAS),
∴S△FAM=S△ABN,
∴S△ABC=S四边形FNCM,
∵在△ABC中,∠ACB=90°,
∴AC2+BC2=AB2,
∵AC+BC=6,
∴(AC+BC)2=AC2+BC2+2ACBC=36,
∴AB2+2ACBC=36,
∵AB2﹣2S△ABC=10.5,
∴AB2﹣ACBC=10.5,
∴3AB2=57,
∴2AB2=38,
∴阴影部分面积为=38﹣10.5×2=17,
故答案为:17.


科目:初中数学 来源: 题型:
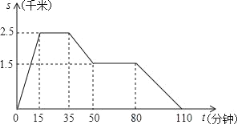
【题目】一天,王亮同学从家里跑步到体育馆,在那里锻炼了一阵后又走到某书店去买书,然后散步走回家如图反映的是在这一过程中,王亮同学离家的距离s(千米)与离家的时间t(分钟)之间的关系,请根据图象解答下列问题:
(1)体育馆离家的距离为多少千米,书店离家的距离为多少千米;王亮同学在书店待了多少分钟.
(2)分别求王亮同学从体育馆走到书店的平均速度和从书店出来散步回家的平均速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=6,BC=8,将矩形ABCD沿CE折叠后,使点D恰好落在对角线AC上的点F处.
(1)求EF的长;
(2)求梯形ABCE的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在利用正六面体骰子进行频率估计概率的实验中,小闽同学统计了某一结果朝上的频率,绘出的统计图如图所示,则符合图中情况的可能是( )
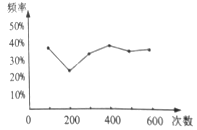
A. 朝上的点数是6的概率B. 朝上的点数是偶数的概率
C. 朝上的点数是小于4的概率D. 朝上的点数是3的倍数的概率
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一艘观光游船从港口A处以北偏东60°的方向出港观光,航行80海里至C处时发生了侧翻沉船事故,立即发生了求救信号,一艘在港口正东方向B处的海警船接到求救信号,测得事故船在它的北偏东37°方向,马上以40海里/时的速度前往救援,求海警船到达事故船C处所需的大约时间.(参考数据:sin53°≈0.8,cos53°≈0.6)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,点A,B,C,D的坐标分别是(1,7),(1,1),(4,1),(6,1).若以C,D,E(E在格点上)为顶点的三角形与△ABC相似,则点E的坐标不可能是( )
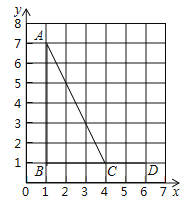
A. (6,0) B. (4,2) C. (6,5) D. (6,3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=kx+8(k<0)交y轴于点A,交x轴于点B.将△AOB关于直线AB翻折得到△APB.过点A作AC∥x轴交线段BP于点C,在AC上取点D,且点D在点C的右侧,连结BD.
(1)求证:AC=BC
(2)若AC=10.
①求直线AB的表达式.
②若△BCD是以BC为腰的等腰三角形,求AD的长.
(3)若BD平分∠OBP的外角,记△APC面积为S1,△BCD面积为S2,且![]() =
=![]() ,则
,则![]() 的值为______(直接写出答案)
的值为______(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
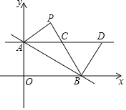
【题目】已知: A 0,1 , B 2, 0 , C 4, 3 .
(1)求△ABC 的面积;
(2)设点 P 在坐标轴上,且△ABC 和△ABP 的面积相等,直接写出 P 的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
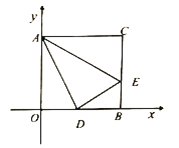
【题目】如图,在平面直角坐标系![]() 中,四边形
中,四边形![]() 为边长为6的正方形,点
为边长为6的正方形,点![]() 为
为![]() 的中点,
的中点,![]() .动点
.动点![]() 在线段
在线段![]() 和
和![]() 上运动,另一动点
上运动,另一动点![]() 在线段
在线段![]() 上运动.
上运动.
用学过的知识解决下列问题:
(1)①填空:点![]() 的坐标____________________;
的坐标____________________;
②求三角形![]() 的面积;
的面积;
(2)求点![]() 在运动过程中,
在运动过程中,![]() 与
与![]() 的数量关系;
的数量关系;
(3)两个动点![]() 在运动过程中,是否存在使线段
在运动过程中,是否存在使线段![]() 的长等于2的时刻,如果存在,求出此时点
的长等于2的时刻,如果存在,求出此时点![]() 坐标;如果不存在,请你说明理由.
坐标;如果不存在,请你说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com