
【题目】如图,在![]() 中,
中,![]() ,点
,点![]() 在
在![]() 的内部,连接
的内部,连接![]() ,
,![]() ,
,![]() ,若
,若![]() ,
,![]() ,则
,则![]() 的长为__________.
的长为__________.
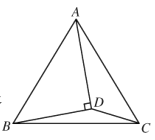
【答案】9
【解析】
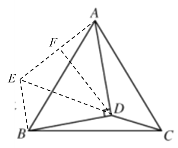
将△ADC绕点A顺时针旋转到△AEB,连接DE,根据旋转的性质证明△AED∽△ABC,利用相似三角形的性质结合∠ADB=90°推出∠EBD=90°,过点D作DF⊥AE,证明△EFD≌△EBD,得到BE=EF,根据![]() ,算出AF=3,在△AFD中,利用勾股定理算出AD,再在△ABD中利用勾股定理算出AC.
,算出AF=3,在△AFD中,利用勾股定理算出AD,再在△ABD中利用勾股定理算出AC.
解:将△ADC绕点A顺时针旋转到△AEB,连接DE,
由题意可得:BD=6,∠ADC=∠AEB=2∠ABC,∠DAC=∠EAB,
∴∠EAD=∠BAC,
又∵AE=AD,AB=AC,
可知:△AED∽△ABC,
∴∠AED=∠ADE=∠BED=∠ABC=![]() ∠ADC=
∠ADC=![]() ∠AEB,
∠AEB,
∵∠ADB=∠ADE+∠BDE=90°,
∴∠BED+∠BDE=90°,
∴∠EBD=90°,
过点D作DF⊥AE,
∵∠BED=∠AED,
∴DB=DE=6,
在△EFD和△EBD中,
 ,
,
∴△EFD≌△EBD(AAS),
∴BE=EF,
∵![]() ,
,
设CD=x,
∴BE=EF=x,AD=AE=x+3,
∴AF=3,
在△AFD中,
AD=![]() ,
,
∴AC=AB=![]() .
.
故答案为:9.


 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:
【题目】随着网购的日益盛行,物流行业已逐渐成为运输业的主力,已知某大型物流公司有A、B两种型号的货车,A型货车的满载量是B型货车满载量的2倍多4吨,在两车满载的情况下,用A型货车载1400吨货物与用B型货车载560吨货物的用车数量相同.
(1)1辆A型货车和1辆B型货车的满载量分别是多少?
(2)该物流公司现有120吨货物,可以选择上述两种货车运送,在满载的情况下,有几种方案可以一次性运完?
查看答案和解析>>
科目:初中数学 来源: 题型:
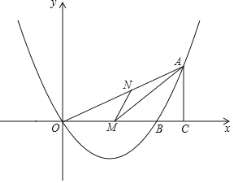
【题目】如图,已知二次函数 y=ax2+bx 的图象与 x 轴交于点 O(0,0)和 点 B,抛物线的对称轴是直线 x=3.点 A 是抛物线在第一象限上的一个动点, 过点 A 作 AC⊥x 轴,垂足为 C.S△AOB=3S△ABC,AC2=OCBC.
(1)求该二次函数的解析式;
(2)抛物线的对称轴与 x 轴交于点 M.连接 AM,点 N 是线段 OA 上的一点.当 ∠AMN=∠AOM 时,求点 N 的坐标;
(3)点 P 是抛物线上的一个动点.点 Q 是 y 轴上的一动点.当以 A,B,P,Q 四个点为顶点的四边形为平行四边形时,直接写出点 P 坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
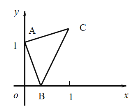
【题目】如右图,点A的坐标为(0,1),点B是x轴正半轴上的一动点,以AB为边作等腰直角△ABC,使∠BAC=90°,如果点B的横坐标为x,点C的纵坐标为y,那么表示y与x的函数关系的图像大致是( )
A.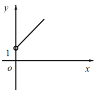 B.
B.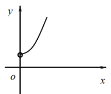
C.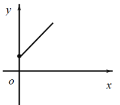 D.
D.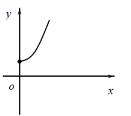
查看答案和解析>>
科目:初中数学 来源: 题型:
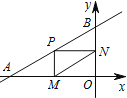
【题目】如图,直线![]() 与x轴、y轴分别交于A、B两点,点P是第二象限图象上一动点,PM⊥x轴于点M,PN⊥y轴于点N,连接MN,在点P的运动过程中,线段MN长度的最小值是________.
与x轴、y轴分别交于A、B两点,点P是第二象限图象上一动点,PM⊥x轴于点M,PN⊥y轴于点N,连接MN,在点P的运动过程中,线段MN长度的最小值是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在平面直角坐标系中,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,
,![]() (点
(点![]() 在点
在点![]() 的右侧),点
的右侧),点![]() 为抛物线的顶点,点
为抛物线的顶点,点![]() 的纵坐标为-2.
的纵坐标为-2.
(1)如图1,求此抛物线的解析式;
(2)如图2,点![]() 是第一象限抛物线上一点,连接
是第一象限抛物线上一点,连接![]() ,过点
,过点![]() 作
作![]() 轴交
轴交![]() 于点
于点![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() ,
,![]() 的长为
的长为![]() ,求
,求![]() 与
与![]() 的函数关系式(不要求写出自变量
的函数关系式(不要求写出自变量![]() 的取值范围);
的取值范围);
(3)如图3,在(2)的条件下,点![]() 在
在![]() 上,且
上,且![]() ,点
,点![]() 的横坐标大于3,连接
的横坐标大于3,连接![]() ,
,![]() ,
,![]() ,且
,且![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,若
,若![]() ,求点
,求点![]() 的坐标.
的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,AB=AC,AD是BC边上的中线,点E是AD上一点,过点B作BF∥EC,交AD的延长线于点F,连接BE,CF.
(1)求证:△BDF≌△CDE;
(2)当ED与BC满足什么数量关系时,四边形BECF是正方形?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,已知抛物线y=﹣![]() x2+
x2+![]() x+2
x+2![]() 与x轴交于A、B两点,与y轴交于C点,抛物线的顶点为Q,连接BC.
与x轴交于A、B两点,与y轴交于C点,抛物线的顶点为Q,连接BC.
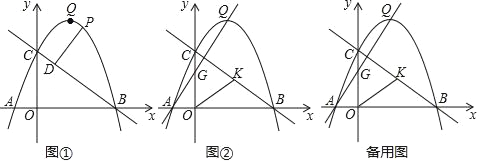
(1)求直线BC的解析式;
(2)点P是直线BC上方抛物线上的一点,过点P作PD⊥BC于点D,在直线BC上有一动点M,当线段PD最大时,求PM+![]() MB最小值;
MB最小值;
(3)如图②,直线AQ交y轴于G,取线段BC的中点K,连接OK,将△GOK沿直线AQ平移得△G′O'K′,将抛物线y=﹣![]() x2+
x2+![]() x+2
x+2![]() 沿直线AQ平移,记平移后的抛物线为y′,当抛物线y′经过点Q时,记顶点为Q′,是否存在以G'、K'、Q'为顶点的三角形是等腰三角形?若存在,求出点G′的坐标;若不存在,请说明理由.
沿直线AQ平移,记平移后的抛物线为y′,当抛物线y′经过点Q时,记顶点为Q′,是否存在以G'、K'、Q'为顶点的三角形是等腰三角形?若存在,求出点G′的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com