
【题目】在平面直角坐标系xOy中,已知点A(-2,0),B(2,0),点P在直线![]() 上,若△ABP是直角三角形,则点P的坐标为______________.
上,若△ABP是直角三角形,则点P的坐标为______________.
【答案】(1,![]() ),(-1,-
),(-1,-![]() ),(2,
),(2,![]() ),(-2,-
),(-2,-![]() )
)
【解析】
设P点的坐标是(x,![]() x)有三种类型:①∠APB=90°,②∠PAB=90°,③∠ABP=90°,根据点的坐标和勾股定理求出x即可.
x)有三种类型:①∠APB=90°,②∠PAB=90°,③∠ABP=90°,根据点的坐标和勾股定理求出x即可.
∵点P在直线y=![]() x上,
x上,
∴设P点的坐标是(x,![]() x)
x)
有三种类型:
①如图1,当∠APB=90°时,
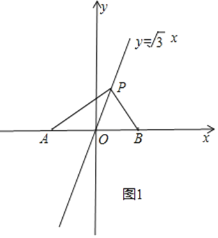
∵A(-2,0),B(2,0),P(x,![]() x),
x),
∴由勾股定理得:AP2+BP2=AB2,
即(-2-x)2+(0-![]() x)2+(x-2)2+(
x)2+(x-2)2+(![]() x-0)2=(2+2)2,
x-0)2=(2+2)2,
解得:x=±1,
即此时点P的坐标是(1,![]() )或(-1,-
)或(-1,-![]() );
);
②如图2,当∠PAB=90°时,
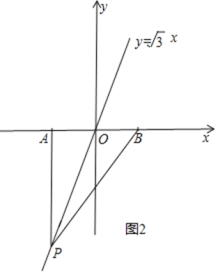
∵A(-2,0),B(2,0),P(x,![]() x),
x),
∴P点的横坐标是-2,纵坐标是-2![]() ,即点P的坐标是(-2,-2
,即点P的坐标是(-2,-2![]() );
);
③当∠ABP=90°时,
点P的坐标是(2,2![]() ),
),
故答案为:(1,![]() )或(-1,-
)或(-1,-![]() )或(-2,-2
)或(-2,-2![]() )或(2,2
)或(2,2![]() ).
).


 百年学典课时学练测系列答案
百年学典课时学练测系列答案科目:初中数学 来源: 题型:
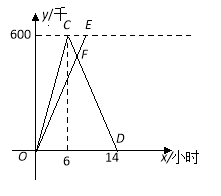
【题目】A,B两城相距600千米,甲、乙两车同时从A城出发驶向B城,甲车到达B城后立即返回.如图是它们离A城的距离y(千米)与行驶时间 x(小时)之间的函数图象.
(1)求甲车行驶过程中y与x之间的函数解析式,并写出自变量x的取值范围;
(2)当它们行驶了7小时时,两车相遇,求乙车的速度及乙车行驶过程中y与x之间的函数解析式,并写出自变量x的取值范围;
(3)当两车相距100千米时,求甲车行驶的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
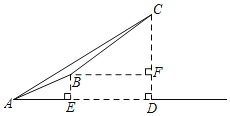
【题目】金佛山是巴蜀四大名山之一游客上金佛山有两种方式:一种是从西坡上山,如图,先从A沿登山步道走到点B,再沿索道乘坐缆车到点C;另一种是从北坡景区沿着盘山公路开车上山到点C.已知在点A处观测点C,得仰角∠CAD=37°,且A、B的水平距离AE=1000米,索道BC的坡度i=1:![]() ,长度为2600米,CD⊥AD于点D,BF⊥CD于点F则BE的高度为(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°=0.75,
,长度为2600米,CD⊥AD于点D,BF⊥CD于点F则BE的高度为(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°=0.75,![]() =1.73)( )
=1.73)( )
A.2436.8米B.2249.6米C.1036.8米D.1136.8米
查看答案和解析>>
科目:初中数学 来源: 题型:
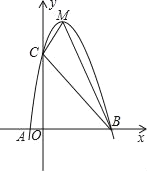
【题目】已知,如图,二次函数y=ax2+bx+c的图象与x轴交于A、B两点,其中A点坐标为(﹣1,0),点C(0,5),另抛物线经过点(1,8),M为它的顶点.
(1)求抛物线的解析式;
(2)求△MCB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于任意的实数m,n,定义运算“∧”,有m∧n=![]() .
.
(1)计算:3∧(-1);
(2)若![]() ,
,![]() ,求m∧n (用含x的式子表示);
,求m∧n (用含x的式子表示);
(3)若![]() ,
,![]() , m∧n=-2 ,求x的值 .
, m∧n=-2 ,求x的值 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 经过点
经过点![]() 和
和![]() .下列结论:①
.下列结论:①![]() ;②
;②![]() ;③当
;③当![]() 时,抛物线与
时,抛物线与![]() 轴必有一个交点在点
轴必有一个交点在点![]() 的右侧;④抛物线的对称轴为
的右侧;④抛物线的对称轴为![]() .
.
其中结论正确的个数有( )
A.4个B.3个C.2个D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
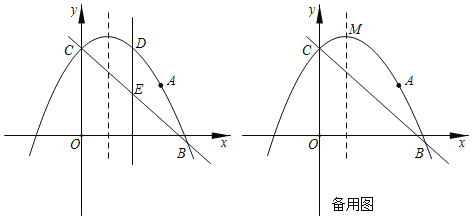
【题目】如图,抛物线![]() 过点
过点![]() ,且与直线
,且与直线![]() 交于B、C两点,点B的坐标为
交于B、C两点,点B的坐标为![]() .
.
(1)求抛物线的解析式;
(2)点D为抛物线上位于直线![]() 上方的一点,过点D作
上方的一点,过点D作![]() 轴交直线
轴交直线![]() 于点E,点P为对称轴上一动点,当线段
于点E,点P为对称轴上一动点,当线段![]() 的长度最大时,求
的长度最大时,求![]() 的最小值;
的最小值;
(3)设点M为抛物线的顶点,在y轴上是否存在点Q,使![]() ?若存在,求点Q的坐标;若不存在,请说明理由.
?若存在,求点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com