
【题目】对于任意的实数m,n,定义运算“∧”,有m∧n=![]() .
.
(1)计算:3∧(-1);
(2)若![]() ,
,![]() ,求m∧n (用含x的式子表示);
,求m∧n (用含x的式子表示);
(3)若![]() ,
,![]() , m∧n=-2 ,求x的值 .
, m∧n=-2 ,求x的值 .
【答案】(1)3;(2)1-x或![]() ;(3)
;(3)![]() 或
或![]()
【解析】
(1)根据新定义的运算法则进行计算即可;
(2)根据新定义的运算法则代入,然后根据x的取值范围不同分情况讨论计算;
(3)根据新定义的运算法则代入,然后根据x的取值范围不同分情况讨论计算即可.
(1)![]()
(2)当x≤-2时,m=1-x,n=-x-2; m∧n=1-x;
当x≥1时,m=x-1,n=x+2; m∧n=2+x;
当-2<x<1时,m=1-x,n=x+2,![]() ;
;
①当-2<x≤-![]() 时,
时,![]() ;
;
②当-![]() <x<1时,
<x<1时,![]()
答:m∧n的值为1-x或x+2.
(3)把m=x2+2x-3,n=-x-3代入m∧n=![]() ,得:
,得:
m∧n=![]()
①当x≤-3或x≥0时,m∧n=x2+2x-3=-2
解得x1=-1+![]() ,x2=-1-
,x2=-1-![]() (不合题意,舍去)
(不合题意,舍去)
②当-3<x<0时,m∧n=-x-3=-2;解得x3=-1;
综上所述,x=-1+![]() 或-1.
或-1.
答:x的值为-1+![]() 或-1.
或-1.


科目:初中数学 来源: 题型:
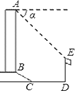
【题目】如图,某办公大楼正前方有一根高度是15米的旗杆ED,从办公大楼顶端A测得旗杆顶端E的俯角α是45°,旗杆底端D到大楼前梯坎底边的距离DC是20米,梯坎坡长BC是12米,梯坎坡度i=1:![]() ,则大楼AB的高度为________米.(精确到0.1米,参考数据:
,则大楼AB的高度为________米.(精确到0.1米,参考数据:![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
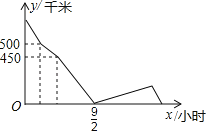
【题目】甲、乙两人驾车分别从A、B两地相向而行,乙出发半小时后甲出发,甲出发1.5小时后汽车出现故障,于是甲停下修车,半小时后甲修好后继续沿原路按原速与乙相遇,相遇后甲随即调头以原速返回A地,乙也继续向A地行驶,甲、乙两车之间的距离(y/千米)与甲驾车时间x(小时)之间的关系如图所示,当乙到达A地时,甲距离B地_____千米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于二次函数y=x2+2x+3的图象有以下说法:其中正确的个数是( )
①它开口向下;②它的对称轴是过点(﹣1,3)且平行于y轴的直线;③它与x轴没有公共点;④它与y轴的交点坐标为(3,0).
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知点A(-2,0),B(2,0),点P在直线![]() 上,若△ABP是直角三角形,则点P的坐标为______________.
上,若△ABP是直角三角形,则点P的坐标为______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形![]() 是菱形,
是菱形,![]() ,点
,点![]() 从
从![]() 点出发,沿
点出发,沿![]() 运动,过点
运动,过点![]() 作直线
作直线![]() 的垂线,垂足为
的垂线,垂足为![]() ,设点
,设点![]() 运动的路程为
运动的路程为![]() ,
,![]() 的面积为
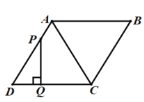
的面积为![]() ,则下列图象能正确反映
,则下列图象能正确反映![]() 与
与![]() 之间的函数关系的是( ).
之间的函数关系的是( ).
A.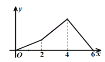 B.
B.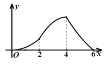 C.
C.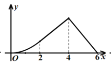 D.
D.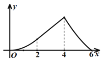
查看答案和解析>>
科目:初中数学 来源: 题型:
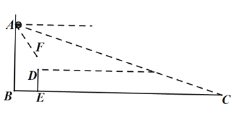
【题目】如图,在教室前面墙壁![]() 处安装了一个摄像头,当恰好观测到后面墙壁与底面交接处点
处安装了一个摄像头,当恰好观测到后面墙壁与底面交接处点![]() 时,摄像头俯角约为
时,摄像头俯角约为![]() ,受安装支架限制,摄像头观测的俯角最大约为
,受安装支架限制,摄像头观测的俯角最大约为![]() ,已知摄像头安装点高度
,已知摄像头安装点高度![]() 约为
约为![]() 米,摄像头与安装的墙壁之间距离忽略不计,
米,摄像头与安装的墙壁之间距离忽略不计,
![]() 求教室的长(教室前后墙壁之间的距离
求教室的长(教室前后墙壁之间的距离![]() 的值);
的值);
![]() 若第一排桌子前边缘与前面墙壁的距离
若第一排桌子前边缘与前面墙壁的距离![]() 为
为![]() 米, 桌子的高度
米, 桌子的高度![]() 为
为![]() 米,那么第一排桌子是否在监控范围内?如果不在,应该怎样移动? (
米,那么第一排桌子是否在监控范围内?如果不在,应该怎样移动? (![]() ,精确到
,精确到![]() 米)
米)
查看答案和解析>>
科目:初中数学 来源: 题型:
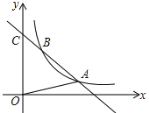
【题目】如图,一次函数的图象与y轴交于C(0,8),且与反比例函数y=![]() (x>0)的图象在第一象限内交于A(3,a),B(1,b)两点.
(x>0)的图象在第一象限内交于A(3,a),B(1,b)两点.
⑴求△AOC的面积;
⑵若![]() =4,求反比例函数和一次函数的解析式.
=4,求反比例函数和一次函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平行四边形ABCD中,对角线AC,BD交于点O,E是边AD上的一个动点(与点A,D不重合),连接EO并延长,交BC于点F,连接BE,DF.下列说法:
① 对于任意的点E,四边形BEDF都是平行四边形;
② 当∠ABC>90°时,至少存在一个点E,使得四边形BEDF是矩形;
③ 当AB<AD时,至少存在一个点E,使得是四边形BEDF是菱形;
④ 当∠ADB=45°时,至少存在一个点E,使得是四边形BEDF是正方形.
所有正确说法的序号是:_________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com