
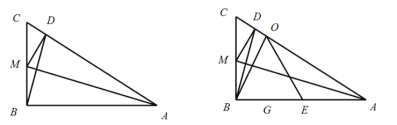
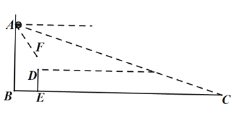
【题目】如图,已知:在直角![]() 中,
中,![]() ,点
,点![]() 在边
在边![]() 上,且
上,且![]() 如果将
如果将![]() 沿
沿![]() 所在的直线翻折,点
所在的直线翻折,点![]() 恰好落在边
恰好落在边![]() 上的点
上的点![]() 处,点
处,点![]() 为
为![]() 边上的一个动点,联结
边上的一个动点,联结![]() ,以
,以![]() 圆心,
圆心,![]() 为半径作⊙
为半径作⊙![]() ,交线段
,交线段![]() 于点
于点![]() 和点
和点![]() ,作
,作![]() 交⊙
交⊙![]() 于点
于点![]() ,
,![]() 交线段
交线段![]() 于点
于点![]() .
.
(1)求点![]() 到点
到点![]() 和直线
和直线![]() 的距离
的距离
(2)如果点![]() 平分劣弧
平分劣弧![]() ,求此时线段
,求此时线段![]() 的长度
的长度
(3)如果![]() 为等腰三角形,以
为等腰三角形,以![]() 为圆心的⊙
为圆心的⊙![]() 与此时的⊙
与此时的⊙![]() 相切,求⊙
相切,求⊙![]() 的半径
的半径
【答案】(1) ![]() ,
,![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 或20.
或20.
【解析】
(1)设BD与AM交于点N,那么∠BNM=90°,BN=DN,然后解直角三角形即可解答;
(2)先确定∠CAB的正弦值,再设BG=3m、OG=4m建立方程求得m;再运用解直角三角形求得BE,最后利用AE=AB-BE即可求解;
(3)先求出△AOE为等腰三角形时圆O的半径及圆心距;然后就圆A与圆O是内切还是外切分类讨论求解即可.
解:(1)如图:设BD与AM交于点N,那么∠BNM=90°,BN=DN

∵Rt△ABM中,AB=12,BM=4,
∴tan∠2=![]() , cos∠2=
, cos∠2=![]()
∵∠1+∠BMN=90°,∠2+∠BMN=90°,
∴∠1=∠2.
∵Rt△BMN中,BM=4,
∴BN=BM·cos∠1=![]()
∴BD=2BN=![]()
如图所示:作DH⊥AB于H,
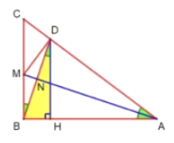
∴DH∥CB
∴∠BDH=∠MBN
∴DH=BD·cos∠BDH=![]() ×
×![]() =
=![]() ;
;
(2)∵在Rt△ADH中,DH=![]() ,AD=AB=12,
,AD=AB=12,
∴sin∠CAB=![]()
如图所示:因为点F平分弧BE,
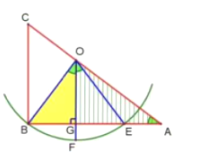
∴OF⊥BE,BG=EG
在Rt△BOG中,已知∠BOF=∠BAC,设BG=3m,OG=4m.
在Rt△AOG中,由tan∠A=![]() =
=![]() ,
,
解得m=![]()
∴AE=AB-BE=12-6m=![]() ;
;
(3)第一步,求△AOE为等腰三角形时圆O的半径,
∵△AOE是钝角三角形,
∴只存在EO=EA的情况。
如图所示:作EK⊥AC于K

在Rt△AEK中,设EK=3n,则AK=4n,EA=5n.
如图所示:作OP⊥AB于P

在Rt△AOP中,OA=2AK=8n,AP=![]() OA=
OA=![]()
∴PE=AP-AE=![]() -5n=
-5n=![]()
由AB=2PE+EA=![]() +5n=12.解得:n=
+5n=12.解得:n=![]() .
.
∴ro=OE=5n=![]() ,圆心距d=OA=
,圆心距d=OA=![]()
第二步,分两种情况讨论圆A与圆O相切.
①如图所示,当圆A与圆O外切时,ro+ra=d,
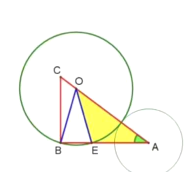
所以ra =d-ro=![]() ;
;
②如图所示,当圆A与圆O内切时ra-ro=d

所以ra=d+ro=![]() .
.


科目:初中数学 来源: 题型:
【题目】新华文具店的某种毛笔每支售价![]() 元,书法练习本每本售价
元,书法练习本每本售价![]() 元,该文具店为促销制定了两种优惠办法:
元,该文具店为促销制定了两种优惠办法:
甲:买一支毛笔就赠送一本书法练习本;
乙:按购买金额打九折付款.
实验中学欲为校书法兴趣小组购买这种毛笔![]() 支,书法练习本
支,书法练习本![]()
![]() 本,
本,
(1)请写出用甲种优惠办法实际付款金额![]() 甲(元)与
甲(元)与![]() (本)之间的函数关系式;
(本)之间的函数关系式;
(2)请写出用乙种优惠办法实际付款金额![]() 乙(元)与
乙(元)与![]() (本)之间的函数关系式;
(本)之间的函数关系式;
(3)若购买同样多的书法练习本时,你会选择哪种优惠办法付款更省钱.
查看答案和解析>>
科目:初中数学 来源: 题型:
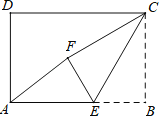
【题目】如图,在矩形ABCD中,AB=3,CB=2,点E为线段AB上的动点,将△CBE沿CE折叠,使点B落在矩形内点F处,下列结论正确的是_____(写出所有正确结论的序号)
①当E为线段AB中点时,AF∥CE;
②当E为线段AB中点时,AF=![]() ;
;
③当A、F、C三点共线时,AE=![]() ;
;
④当A、F、C三点共线时,△CEF≌△AEF.
查看答案和解析>>
科目:初中数学 来源: 题型:
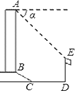
【题目】如图,某办公大楼正前方有一根高度是15米的旗杆ED,从办公大楼顶端A测得旗杆顶端E的俯角α是45°,旗杆底端D到大楼前梯坎底边的距离DC是20米,梯坎坡长BC是12米,梯坎坡度i=1:![]() ,则大楼AB的高度为________米.(精确到0.1米,参考数据:
,则大楼AB的高度为________米.(精确到0.1米,参考数据:![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
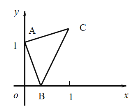
【题目】如右图,点A的坐标为(0,1),点B是x轴正半轴上的一动点,以AB为边作等腰直角△ABC,使∠BAC=90°,如果点B的横坐标为x,点C的纵坐标为y,那么表示y与x的函数关系的图像大致是( )
A. B.
B.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列解题过程:
例:若代数式![]() ,求a的取值.
,求a的取值.
解:原式=![]() ,
,
当a<2时,原式=(2-a)+(4-a)=6-2a=2,解得a=2(舍去);
当2≤a<4时,原式=(a-2)+(4-a)=2=2,等式恒成立;
当a≥4时,原式=(a-2)+(a-4)=2a-6=2,解得a=4;
所以,a的取值范围是2≤a≤4.
上述解题过程主要运用了分类讨论的方法,请你根据上述理解,解答下列问题:
(1)当3≤a≤7时,化简:![]() =_________;
=_________;
(2)请直接写出满足![]() =5的a的取值范围__________;
=5的a的取值范围__________;
(3)若![]() =6,求a的取值.
=6,求a的取值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在平面直角坐标系中,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,
,![]() (点
(点![]() 在点
在点![]() 的右侧),点
的右侧),点![]() 为抛物线的顶点,点
为抛物线的顶点,点![]() 的纵坐标为-2.
的纵坐标为-2.
(1)如图1,求此抛物线的解析式;
(2)如图2,点![]() 是第一象限抛物线上一点,连接
是第一象限抛物线上一点,连接![]() ,过点
,过点![]() 作
作![]() 轴交
轴交![]() 于点
于点![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() ,
,![]() 的长为
的长为![]() ,求
,求![]() 与
与![]() 的函数关系式(不要求写出自变量
的函数关系式(不要求写出自变量![]() 的取值范围);
的取值范围);
(3)如图3,在(2)的条件下,点![]() 在
在![]() 上,且
上,且![]() ,点
,点![]() 的横坐标大于3,连接
的横坐标大于3,连接![]() ,
,![]() ,
,![]() ,且
,且![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,若
,若![]() ,求点
,求点![]() 的坐标.
的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人驾车分别从A、B两地相向而行,乙出发半小时后甲出发,甲出发1.5小时后汽车出现故障,于是甲停下修车,半小时后甲修好后继续沿原路按原速与乙相遇,相遇后甲随即调头以原速返回A地,乙也继续向A地行驶,甲、乙两车之间的距离(y/千米)与甲驾车时间x(小时)之间的关系如图所示,当乙到达A地时,甲距离B地_____千米.
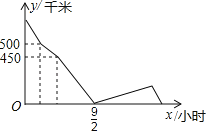
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在教室前面墙壁![]() 处安装了一个摄像头,当恰好观测到后面墙壁与底面交接处点
处安装了一个摄像头,当恰好观测到后面墙壁与底面交接处点![]() 时,摄像头俯角约为
时,摄像头俯角约为![]() ,受安装支架限制,摄像头观测的俯角最大约为
,受安装支架限制,摄像头观测的俯角最大约为![]() ,已知摄像头安装点高度
,已知摄像头安装点高度![]() 约为
约为![]() 米,摄像头与安装的墙壁之间距离忽略不计,
米,摄像头与安装的墙壁之间距离忽略不计,
![]() 求教室的长(教室前后墙壁之间的距离
求教室的长(教室前后墙壁之间的距离![]() 的值);
的值);
![]() 若第一排桌子前边缘与前面墙壁的距离
若第一排桌子前边缘与前面墙壁的距离![]() 为
为![]() 米, 桌子的高度
米, 桌子的高度![]() 为
为![]() 米,那么第一排桌子是否在监控范围内?如果不在,应该怎样移动? (
米,那么第一排桌子是否在监控范围内?如果不在,应该怎样移动? (![]() ,精确到
,精确到![]() 米)
米)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com