
【题目】探究函数![]() 的图象和性质.洋洋同学根据学习函数的经验,对函数
的图象和性质.洋洋同学根据学习函数的经验,对函数![]() 的图象和性质进行了探究,下面是洋洋的探究过程,请补充完成:
的图象和性质进行了探究,下面是洋洋的探究过程,请补充完成:
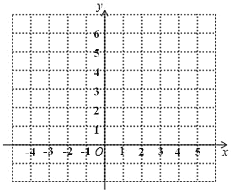
(1)化简函数解析式:当![]() 时,
时,![]() ______,当
______,当![]() 时,
时,![]() ______;
______;
(2)根据(1)的结果,请在所给坐标系中画出函数![]() 的图象;(直尺画图,不用列表)
的图象;(直尺画图,不用列表)
(3)观察函数图象,请写出该函数的一条性质:______.
科目:初中数学 来源: 题型:
【题目】小明为了检验两枚六个面分别刻有点数1、 2、3、4、5、6的正六面体骰子的质量是否都合格,在相同的条件下,同时抛两枚骰子20 00 0次,结果发现两个朝上面的点数和是7的次数为20次.你认为这两枚骰子质量是否都合格(合格标准为:在相同条件下抛骰子时,骰子各个面朝上的机会相等)?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:
材料一:数学上有一种根号内又带根号的数,它们能通过完全平方式及二次根式的性质化去一层(或多层)根号,如:![]()
材料二:配方法是初中数学思想方法中的一种重要的解题方法,配方法的最终目的就是配成完全平方式, 利用完全平方式来解决问题,它的应用非常广泛,在解方程、化简根式、因式分解等方面都经常 用到.
如:![]()
∵![]() ,∴
,∴![]() ,即
,即![]()
∴![]() 的最小值为
的最小值为![]()
阅读上述材料解决下面问题:
(1)![]() ,
,![]() ;
;
(2)求![]() 的最值;
的最值;
(3)已知![]() ,求
,求![]() 的最值.
的最值.
查看答案和解析>>
科目:初中数学 来源: 题型:
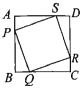
【题目】如图,![]() 四个小球分别从正方形的四个顶点
四个小球分别从正方形的四个顶点![]() 处出发(小球的大小忽略不计),以同样的速度分别沿
处出发(小球的大小忽略不计),以同样的速度分别沿![]() 方向滚动,其终点分别是点
方向滚动,其终点分别是点![]() ,顺次连接四个小球所在的位置,得到四边形
,顺次连接四个小球所在的位置,得到四边形![]() .
.
(1)不论小球滚动多长时间,求证;四边形![]() 总是正方形;
总是正方形;
(2)这个四边形在什么时候面积最大?
(3)在什么时侯四边形![]() 的面积为正方形
的面积为正方形![]() 面积的一半?请说明理由.
面积的一半?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某市近郊有一块长为60米,宽为50米的矩形荒地,地方政府准备在此建一个综合性休闲广场,其中阴影部分为通道,通道的宽度均相等,中间的三个矩形(其中三个矩形的一边长均为a米)区域将铺设塑胶地面作为运动场地.设通道的宽度为x米.

(1)a= (用含x的代数式表示);
(2)若塑胶运动场地总占地面积为 2430平方米,则通道的宽度为多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
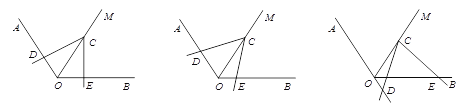
【题目】如图,已知∠AOB=120°,在∠AOB的平分线OM上有一点C,将一个60°角的顶点与点C重合,它的两条边分别与直线OA、OB相交于点D、E.
(1)当∠DCE绕点C旋转到CD与OA垂直时(如图1),请猜想OE+OD与OC的数量关系,并说明理由;
(2)当∠DCE绕点C旋转到CD与OA不垂直时,到达图2的位置,(1)中的结论是否成立?并说明理由;
(3)当∠DCE绕点C旋转到CD与OA的反向延长线相交时,上述结论是否成立?若成立,请给于证明;若不成立,线段OD、OE与OC之间又有怎样的数量关系?请写出你的猜想,不需证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A是函数y=![]() 图象上的一点,已知B(﹣
图象上的一点,已知B(﹣![]() ,﹣
,﹣![]() ),C(
),C(![]() ,
,![]() ).试利用性质:“y=
).试利用性质:“y=![]() 图象上的任意一点P都满足|PB﹣PC|=2
图象上的任意一点P都满足|PB﹣PC|=2![]() ”求解下面问题:作∠BAC的内角平分线AE,过B作AE的垂线交AE于F.当点A在函数y=
”求解下面问题:作∠BAC的内角平分线AE,过B作AE的垂线交AE于F.当点A在函数y=![]() 图象上运动时,点F也总在一图形上运动,该图形为( )
图象上运动时,点F也总在一图形上运动,该图形为( )
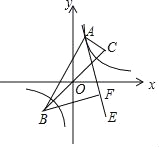
A. 圆 B. 双曲线 C. 抛物线 D. 直线
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com