
【题目】阅读材料:
材料一:数学上有一种根号内又带根号的数,它们能通过完全平方式及二次根式的性质化去一层(或多层)根号,如:![]()
材料二:配方法是初中数学思想方法中的一种重要的解题方法,配方法的最终目的就是配成完全平方式, 利用完全平方式来解决问题,它的应用非常广泛,在解方程、化简根式、因式分解等方面都经常 用到.
如:![]()
∵![]() ,∴
,∴![]() ,即
,即![]()
∴![]() 的最小值为
的最小值为![]()
阅读上述材料解决下面问题:
(1)![]() ,
,![]() ;
;
(2)求![]() 的最值;
的最值;
(3)已知![]() ,求
,求![]() 的最值.
的最值.
科目:初中数学 来源: 题型:
【题目】甲、乙两人在一条笔直的道路上相向而行,甲骑自行车从A地到B地,乙驾车从B地到A地,他们分别以不同的速度匀速行驶,已知甲先出发6分钟后,乙才出发,在整个过程中,甲、乙两人的距离y(千米)与甲出发的时间x(分)之间的关系如图所示,当乙到达终点A时,甲还需 分钟到达终点B.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一座抛物线形拱桥,在正常水位时水面AB的宽为20米,如果水位上升3米,则水面CD的宽是10米.

(1)建立如图所示的直角坐标系,求此抛物线的解析式;
(2)当水位在正常水位时,有一艘宽为6米的货船经过这里,船舱上有高出水面3.6米的长方体货物(货物与货船同宽).问:此船能否顺利通过这座拱桥?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(14分)如图1,已知点B(0,6),点C为x轴上一动点,连接BC,△ODC和△EBC都是等边三角形.
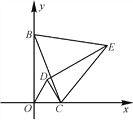
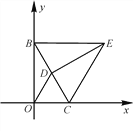
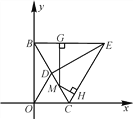
图1 图2 图3
(1)求证:DE=BO;
(2)如图2,当点D恰好落在BC上时.
①求OC的长及点E的坐标;
②在x轴上是否存在点P,使△PEC为等腰三角形?若存在,写出点P的坐标;若不存在,说明理由;
③如图3,点M是线段BC上的动点(点B,C除外),过点M作MG⊥BE于点G,MH⊥CE于点H,当点M运动时,MH+MG的值是否发生变化?若不会变化,直接写出MH+MG的值;若会变化,简要说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=﹣x2+2x+3.
(1)求其开口方向、对称轴、顶点坐标,并画出这个函数的图象;
(2)根据图象,直接写出:①当函数值y为正数时,自变量x的取值范围;
②当﹣2<x<2时,函数值y的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
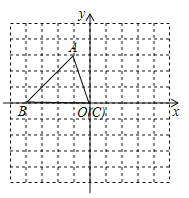
【题目】(2016黑龙江省齐齐哈尔市)如图,平面直角坐标系内,小正方形网格的边长为1个单位长度,△ABC的三个顶点的坐标分别为A(﹣1,3),B(﹣4,0),C(0,0)
(1)画出将△ABC向上平移1个单位长度,再向右平移5个单位长度后得到的△A1B1C1;
(2)画出将△ABC绕原点O顺时针方向旋转90°得到△A2B2O;
(3)在x轴上存在一点P,满足点P到A1与点A2距离之和最小,请直接写出P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]()
抛物线 | 顶点坐标 | 与x轴交点坐标 | 与y轴交点坐标 | |
抛物线 | A(____) | B(____) | (1,0) | (0,-3) |
(1)补全表中A,B两点的坐标,并在所给的平面直角坐标系中,画出抛物线![]()
(2)结合图象回答
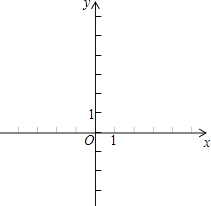
①当x的取值范围为________时,y随x的增大而增大;
②当x________时,![]() ;
;
③当![]() 时,y的取值范围________.
时,y的取值范围________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究函数![]() 的图象和性质.洋洋同学根据学习函数的经验,对函数
的图象和性质.洋洋同学根据学习函数的经验,对函数![]() 的图象和性质进行了探究,下面是洋洋的探究过程,请补充完成:
的图象和性质进行了探究,下面是洋洋的探究过程,请补充完成:
(1)化简函数解析式:当![]() 时,
时,![]() ______,当
______,当![]() 时,
时,![]() ______;
______;
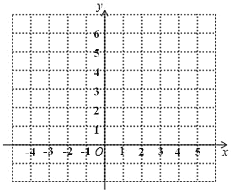
(2)根据(1)的结果,请在所给坐标系中画出函数![]() 的图象;(直尺画图,不用列表)
的图象;(直尺画图,不用列表)
(3)观察函数图象,请写出该函数的一条性质:______.
查看答案和解析>>
科目:初中数学 来源: 题型:
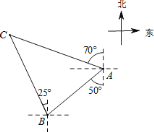
【题目】如图,轮船在![]() 处观测灯塔
处观测灯塔![]() 位于北偏西
位于北偏西![]() 方向上,轮船从
方向上,轮船从![]() 处以每小时
处以每小时![]() 海里的速度沿南偏西
海里的速度沿南偏西![]() 方向匀速航行,
方向匀速航行,![]() 小时后到达码头
小时后到达码头![]() 处,此时,观测灯塔
处,此时,观测灯塔![]() 位于北偏西
位于北偏西![]() 方向上,则灯塔
方向上,则灯塔![]() 与码头
与码头![]() 的距离是____海里.(结果精确到个位,参考数据:
的距离是____海里.(结果精确到个位,参考数据:![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com