
【题目】如图,有一座抛物线形拱桥,在正常水位时水面AB的宽为20米,如果水位上升3米,则水面CD的宽是10米.

(1)建立如图所示的直角坐标系,求此抛物线的解析式;
(2)当水位在正常水位时,有一艘宽为6米的货船经过这里,船舱上有高出水面3.6米的长方体货物(货物与货船同宽).问:此船能否顺利通过这座拱桥?
科目:初中数学 来源: 题型:
【题目】如图,△OAC中,以O为圆心,OA为半径作⊙O,作OB⊥OC交⊙O于B,垂足为O,连接AB交OC于点D,∠CAD=∠CDA.
(1)判断AC与⊙O的位置关系,并证明你的结论;
(2)若OA=5,OD=1,求线段AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() ,
,
![]() 求抛物线与
求抛物线与![]() 轴的交点坐标;
轴的交点坐标;
![]() 求抛物线与
求抛物线与![]() 轴的两个交点及两个交点间的距离.
轴的两个交点及两个交点间的距离.
![]() 求抛物线与
求抛物线与![]() 轴的交点及与
轴的交点及与![]() 轴交点所围成的三角形面积.
轴交点所围成的三角形面积.
![]() 把抛物线
把抛物线![]() 改为顶点式,说明顶点和对称轴.
改为顶点式,说明顶点和对称轴.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明为了检验两枚六个面分别刻有点数1、 2、3、4、5、6的正六面体骰子的质量是否都合格,在相同的条件下,同时抛两枚骰子20 00 0次,结果发现两个朝上面的点数和是7的次数为20次.你认为这两枚骰子质量是否都合格(合格标准为:在相同条件下抛骰子时,骰子各个面朝上的机会相等)?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,图象中所反映的过程是:张强从家跑步去体育场,在那里锻炼了一阵后,又 去早餐店吃早餐,然后散步走回家,其中 x 表示时间,y 表示张强离家的距离。根据图象提供的信息,以下四个说法错误的是( )

A. 体育场离张强家2.5千米 B. 张强在体育场锻炼了15分钟
C. 体育场离早餐店4千米 D. 张强从早餐店回家的平均速度是3千米/小时
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),在平面直角坐标系中,直线![]() 交y轴于点A,交x轴于点B,点C坐标为
交y轴于点A,交x轴于点B,点C坐标为![]() ,作点C关于直线AB的对称点F,连接BF和OF,OF交AC于点E,交AB于点M.
,作点C关于直线AB的对称点F,连接BF和OF,OF交AC于点E,交AB于点M.
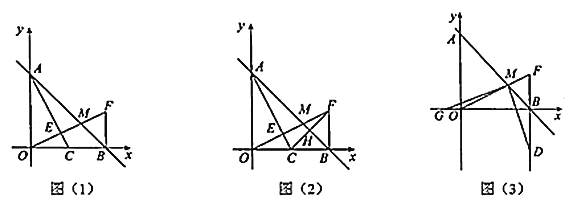
(1)求证:![]() .
.
(2)如图(2),连接CF交AB于点H,求证:![]() .
.
(3)如图(3),若![]() ,G为x轴负半轴上一动点,连接MG,过点M作GM的垂线交FB的延长线于点D,GB-BD的值是否为定值?若是,求其值;若不是,求其取值范围.
,G为x轴负半轴上一动点,连接MG,过点M作GM的垂线交FB的延长线于点D,GB-BD的值是否为定值?若是,求其值;若不是,求其取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ ABC中,∠ABC和∠ACB的平分线相交于点G,过点G作EF ∥BC交AB于E,交AC于F,过点G作GD⊥ AC于D,下列四个结论:①EF = BE+CF;②∠BGC= 90 °+![]() ∠A;③点G到△ ABC各边的距离相等;④设GD =m,AE + AF =n,则S△AEF=
∠A;③点G到△ ABC各边的距离相等;④设GD =m,AE + AF =n,则S△AEF=![]() mn.其中正确的结论有( )
mn.其中正确的结论有( )

A.1 个B.2 个C.3 个D.4 个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:
材料一:数学上有一种根号内又带根号的数,它们能通过完全平方式及二次根式的性质化去一层(或多层)根号,如:![]()
材料二:配方法是初中数学思想方法中的一种重要的解题方法,配方法的最终目的就是配成完全平方式, 利用完全平方式来解决问题,它的应用非常广泛,在解方程、化简根式、因式分解等方面都经常 用到.
如:![]()
∵![]() ,∴
,∴![]() ,即
,即![]()
∴![]() 的最小值为
的最小值为![]()
阅读上述材料解决下面问题:
(1)![]() ,
,![]() ;
;
(2)求![]() 的最值;
的最值;
(3)已知![]() ,求
,求![]() 的最值.
的最值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A是函数y=![]() 图象上的一点,已知B(﹣
图象上的一点,已知B(﹣![]() ,﹣
,﹣![]() ),C(
),C(![]() ,
,![]() ).试利用性质:“y=
).试利用性质:“y=![]() 图象上的任意一点P都满足|PB﹣PC|=2
图象上的任意一点P都满足|PB﹣PC|=2![]() ”求解下面问题:作∠BAC的内角平分线AE,过B作AE的垂线交AE于F.当点A在函数y=
”求解下面问题:作∠BAC的内角平分线AE,过B作AE的垂线交AE于F.当点A在函数y=![]() 图象上运动时,点F也总在一图形上运动,该图形为( )
图象上运动时,点F也总在一图形上运动,该图形为( )
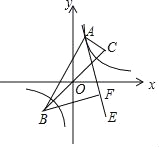
A. 圆 B. 双曲线 C. 抛物线 D. 直线
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com