
【题目】如图,在△ ABC中,∠ABC和∠ACB的平分线相交于点G,过点G作EF ∥BC交AB于E,交AC于F,过点G作GD⊥ AC于D,下列四个结论:①EF = BE+CF;②∠BGC= 90 °+![]() ∠A;③点G到△ ABC各边的距离相等;④设GD =m,AE + AF =n,则S△AEF=
∠A;③点G到△ ABC各边的距离相等;④设GD =m,AE + AF =n,则S△AEF=![]() mn.其中正确的结论有( )
mn.其中正确的结论有( )

A.1 个B.2 个C.3 个D.4 个
【答案】D
【解析】
根据BG,CG分别是∠ABC和∠ACB的平分线,EF ∥BC,可得EB=EG,FG=FC,从而证得①正确;根据三角形内角和定理即可求出②正确;根据角平分线的性质可知点G是△ABC的内心,从而可得③正确;连接AG,结合点G是内心,即可表示出△AEG和△AFG的面积,从而可知④正确.
∵BG,CG分别是∠ABC和∠ACB的平分线,
∴∠EBG=∠GBC,∠FCG=∠GCB
∵EF ∥BC
∴∠EGB=∠GBC,∠FGC=∠GCB
∴∠EBG=∠EGB,∠FCG=∠FGC
∴EB=EG,FG=FC
∴EF = BE+CF
故①正确;
在△ABC中,∠A=180°-(∠ABC+∠ACB)
在△GBC中,![]() ,
,
即![]()
所以②正确;
∵点G是∠ABC和∠ACB的平分线的交点,
∴点G是△ABC的内心
∴点G到△ABC各边的距离相等
故③正确;

连接AG,
∵点G到△ABC各边的距离相等,GD=m,AE+AF=n,
∴![]()
故④正确;
综上答案选D.


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:初中数学 来源: 题型:
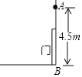
【题目】如图,有一个由传感器A控制的灯,要装在门上方离地面4.5m的墙上,任何东西只要移至该灯5m及5m内,灯就会自动发光,小明身高1.5m,他走到离墙_______的地方灯刚好发光.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一座抛物线形拱桥,在正常水位时水面AB的宽为20米,如果水位上升3米,则水面CD的宽是10米.

(1)建立如图所示的直角坐标系,求此抛物线的解析式;
(2)当水位在正常水位时,有一艘宽为6米的货船经过这里,船舱上有高出水面3.6米的长方体货物(货物与货船同宽).问:此船能否顺利通过这座拱桥?
查看答案和解析>>
科目:初中数学 来源: 题型:
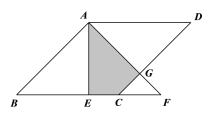
【题目】如图,在菱形ABCD中,AE⊥BC于E,将△ABE沿AE所在直线翻折得△AEF,若AB=2,∠B=45°,则△AEF与菱形ABCD重叠部分(阴影部分)的面积为( ).
A. 2 B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(14分)如图1,已知点B(0,6),点C为x轴上一动点,连接BC,△ODC和△EBC都是等边三角形.
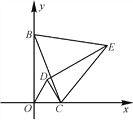
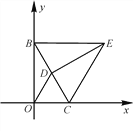
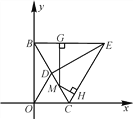
图1 图2 图3
(1)求证:DE=BO;
(2)如图2,当点D恰好落在BC上时.
①求OC的长及点E的坐标;
②在x轴上是否存在点P,使△PEC为等腰三角形?若存在,写出点P的坐标;若不存在,说明理由;
③如图3,点M是线段BC上的动点(点B,C除外),过点M作MG⊥BE于点G,MH⊥CE于点H,当点M运动时,MH+MG的值是否发生变化?若不会变化,直接写出MH+MG的值;若会变化,简要说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=﹣x2+2x+3.
(1)求其开口方向、对称轴、顶点坐标,并画出这个函数的图象;
(2)根据图象,直接写出:①当函数值y为正数时,自变量x的取值范围;
②当﹣2<x<2时,函数值y的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]()
抛物线 | 顶点坐标 | 与x轴交点坐标 | 与y轴交点坐标 | |
抛物线 | A(____) | B(____) | (1,0) | (0,-3) |
(1)补全表中A,B两点的坐标,并在所给的平面直角坐标系中,画出抛物线![]()
(2)结合图象回答
①当x的取值范围为________时,y随x的增大而增大;
②当x________时,![]() ;
;
③当![]() 时,y的取值范围________.
时,y的取值范围________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某养鸡场有2500只鸡准备对外出售.从中随机抽取了一部分鸡,根据它们的质量(单位:![]() ),绘制出如下的统计图①和图②.请根据相关信息,解答下列问题:
),绘制出如下的统计图①和图②.请根据相关信息,解答下列问题:
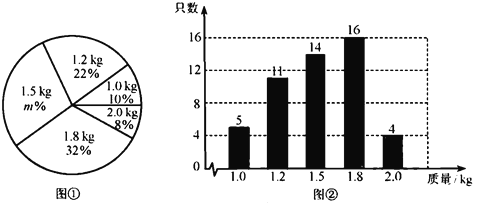
(Ⅰ)图①中![]() 的值为 ;
的值为 ;
(Ⅱ)求统计的这组数据的平均数、众数和中位数;
(Ⅲ) 根据样本数据,估计这2500只鸡中,质量为![]() 的约有多少只?
的约有多少只?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com