
【题目】如图(1),在平面直角坐标系中,直线![]() 交y轴于点A,交x轴于点B,点C坐标为
交y轴于点A,交x轴于点B,点C坐标为![]() ,作点C关于直线AB的对称点F,连接BF和OF,OF交AC于点E,交AB于点M.
,作点C关于直线AB的对称点F,连接BF和OF,OF交AC于点E,交AB于点M.
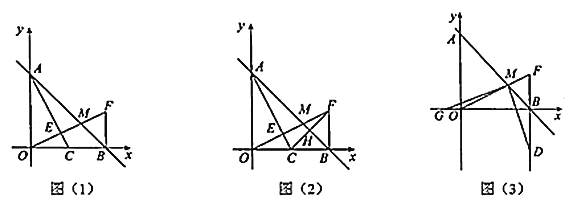
(1)求证:![]() .
.
(2)如图(2),连接CF交AB于点H,求证:![]() .
.
(3)如图(3),若![]() ,G为x轴负半轴上一动点,连接MG,过点M作GM的垂线交FB的延长线于点D,GB-BD的值是否为定值?若是,求其值;若不是,求其取值范围.
,G为x轴负半轴上一动点,连接MG,过点M作GM的垂线交FB的延长线于点D,GB-BD的值是否为定值?若是,求其值;若不是,求其取值范围.
【答案】(1)见解析;(2)见解析;(3)是,![]()
【解析】
(1)先求出A,B的坐标,再通过对称得到FB=BC且垂直x轴,从而证Rt△OAC≌Rt△FOB,得到OF⊥AC.
(2)利用勾股定理和等腰直角三角形的性质分别求出BA,BF,BH即可.
(3)过M点作MN⊥x轴于N点,MH⊥DF于H点,证明直角△MEN≌直角△MDH.
(1)证明![]() 由
由![]() 得
得![]()
![]() ,
,
![]()
![]() .
.
![]() 关于AB对称,
关于AB对称,
![]()
![]() ,
,
![]() .
.
又![]()
![]() .
.
![]()
![]() .
.
![]()
![]() ,
,
![]() ,即
,即![]() .
.
(2)证明:![]() 在
在![]() 中,
中,![]() ,
,
![]()
![]() ,
,
在![]() 中,
中,![]()
![]() ,
,
![]()
![]() .
.
(3)解:GB-BD的值是定值,定值等于![]() .
.
![]()
![]() 直线AB的解析式为
直线AB的解析式为![]() ,
,
点F的坐标为![]() ,直线OF的解析式为
,直线OF的解析式为![]() .
.
解方程组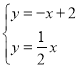 得
得![]() ,
,
![]() .
.
过点M作![]() 轴于点N,
轴于点N,![]() 于点H,如图
于点H,如图
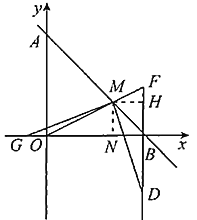
![]()
![]()
![]() 四边形MNBH是正方形,
四边形MNBH是正方形,
![]()
![]()
![]() .
.
又![]()
![]() ,
,
![]() ,
,
![]() .
.
![]() 在
在![]() 和
和![]() 中,
中,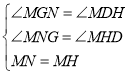 ,
,
![]()
![]() .
.
![]()
![]()
![]() .
.
综上所述,GB-BD的值为定值![]() .
.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AC=BC=8,点P为AB的中点,E为BC上一动点,过P点作FP⊥PE交AC于F点,经过P、E、F三点确定⊙O.
(1)试说明:点C也一定在⊙O上.
(2)点E在运动过程中,∠PEF的度数是否变化?若不变,求出∠PEF的度数;若变化,说明理由.
(3)求线段EF的取值范围,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中,正确的是( )
A. 希望小学初一年级的![]() 名同学中,至少有两个生日相同的概率是
名同学中,至少有两个生日相同的概率是![]()
B. 在投掷骰子时,连投两次点数相同的概率与连投两次点数都为![]() 的概率相等
的概率相等
C. 我们小组共![]() 名同学,他们中肯定有两人在同一月过生日
名同学,他们中肯定有两人在同一月过生日
D. 一个游戏的中奖率是![]() ,买
,买![]() 张奖券,一定会中奖
张奖券,一定会中奖
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘船由A港沿北偏东60°方向航行10km至B港,然后再沿北偏西30°方向航行10km至C港.
(1)求A,C两港之间的距离(结果保留到0.1km,参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732);
≈1.732);
(2)确定C港在A港的什么方向.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一座抛物线形拱桥,在正常水位时水面AB的宽为20米,如果水位上升3米,则水面CD的宽是10米.

(1)建立如图所示的直角坐标系,求此抛物线的解析式;
(2)当水位在正常水位时,有一艘宽为6米的货船经过这里,船舱上有高出水面3.6米的长方体货物(货物与货船同宽).问:此船能否顺利通过这座拱桥?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先来看一个有趣的现象:![]() .这样根号里的因数2经过适当地演变,竟“跑”到了根号的外面,我们不妨把这种现象称为“穿墙”,具有这一性质的数还有许多,如:
.这样根号里的因数2经过适当地演变,竟“跑”到了根号的外面,我们不妨把这种现象称为“穿墙”,具有这一性质的数还有许多,如:![]() ,
,![]() 等.
等.
(1)猜想:![]() ______,并验证你的猜想.
______,并验证你的猜想.
(2)你能只用一个正整数![]() 来表示含有上述规律的等式吗?
来表示含有上述规律的等式吗?
(3)请你另外再写出1个具有“穿墙”性质的数.
查看答案和解析>>
科目:初中数学 来源: 题型:
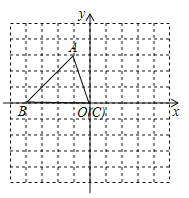
【题目】(14分)如图1,已知点B(0,6),点C为x轴上一动点,连接BC,△ODC和△EBC都是等边三角形.
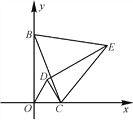
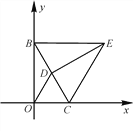
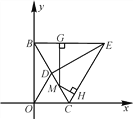
图1 图2 图3
(1)求证:DE=BO;
(2)如图2,当点D恰好落在BC上时.
①求OC的长及点E的坐标;
②在x轴上是否存在点P,使△PEC为等腰三角形?若存在,写出点P的坐标;若不存在,说明理由;
③如图3,点M是线段BC上的动点(点B,C除外),过点M作MG⊥BE于点G,MH⊥CE于点H,当点M运动时,MH+MG的值是否发生变化?若不会变化,直接写出MH+MG的值;若会变化,简要说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2016黑龙江省齐齐哈尔市)如图,平面直角坐标系内,小正方形网格的边长为1个单位长度,△ABC的三个顶点的坐标分别为A(﹣1,3),B(﹣4,0),C(0,0)
(1)画出将△ABC向上平移1个单位长度,再向右平移5个单位长度后得到的△A1B1C1;
(2)画出将△ABC绕原点O顺时针方向旋转90°得到△A2B2O;
(3)在x轴上存在一点P,满足点P到A1与点A2距离之和最小,请直接写出P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列不是一次函数关系的是( )
A.矩形一条边的长固定,面积与另一条边的长的关系
B.矩形一条边的长固定,周长与另一条边的长的关系
C.圆的周长与直径的关系
D.圆的面积与直径的关系
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com