
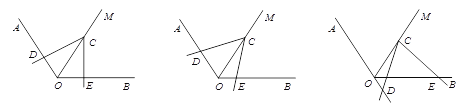
【题目】如图,已知∠AOB=120°,在∠AOB的平分线OM上有一点C,将一个60°角的顶点与点C重合,它的两条边分别与直线OA、OB相交于点D、E.
(1)当∠DCE绕点C旋转到CD与OA垂直时(如图1),请猜想OE+OD与OC的数量关系,并说明理由;
(2)当∠DCE绕点C旋转到CD与OA不垂直时,到达图2的位置,(1)中的结论是否成立?并说明理由;
(3)当∠DCE绕点C旋转到CD与OA的反向延长线相交时,上述结论是否成立?若成立,请给于证明;若不成立,线段OD、OE与OC之间又有怎样的数量关系?请写出你的猜想,不需证明.
【答案】(1)详见解析;(2)(1)中结论仍然成立,理由详见解析;(3)(1)中结论不成立,结论为OE﹣OD=OC,证明详见解析.
【解析】
(1)根据OM是∠AOB的角平分线,可得∠AOB=60°,则∠OCE=30°,再根据30°所对直角边是斜边的一半,得出OD=![]() OC,同理:OE=
OC,同理:OE=![]() OC,即可得出结论;(2)同(1)的方法得到OF+OG=OC,再根据AAS证明△CFD≌△CGE,得出DF=EG,则OF=OD+DF=OD+EG,OG=OE﹣EG,OF+OG=OD+OE,即可得出结论.(3)同(2)的方法得到DF=EG,根据等量代换可得OE﹣OD=OC.
OC,即可得出结论;(2)同(1)的方法得到OF+OG=OC,再根据AAS证明△CFD≌△CGE,得出DF=EG,则OF=OD+DF=OD+EG,OG=OE﹣EG,OF+OG=OD+OE,即可得出结论.(3)同(2)的方法得到DF=EG,根据等量代换可得OE﹣OD=OC.
(1)∵OM是∠AOB的角平分线,
∴∠AOC=∠BOC=![]() ∠AOB=60°,
∠AOB=60°,
∵CD⊥OA,
∴∠ODC=90°,
∴∠OCD=30°,
∴∠OCE=∠DCE﹣∠OCD=30°,
在Rt△OCD中,OD=![]() OC,同理:OE=
OC,同理:OE=![]() OC,
OC,
∴OD+OE=OC,
(2)(1)中结论仍然成立,理由:
过点C作CF⊥OA于F,CG⊥OB于G,如图,
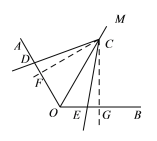
∴∠OFC=∠OGC=90°,
∵∠AOB=120°,
∴∠FCG=60°,
同(1)的方法得,OF=![]() OC,OG=
OC,OG=![]() OC,
OC,
∴OF+OG=OC,
∵CF⊥OA,CG⊥OB,且点C是∠AOB的平分线OM上一点,
∴CF=CG,
∵∠DCE=60°,∠FCG=60°,
∴∠DCF=∠ECG,
∴△CFD≌△CGE,
∴DF=EG,
∴OF=OD+DF=OD+EG,OG=OE﹣EG,
∴OF+OG=OD+EG+OE﹣EG=OD+OE,
∴OD+OE=OC;
(3)(1)中结论不成立,结论为:OE﹣OD=OC,
理由:过点C作CF⊥OA于F,CG⊥OB于G,如图,
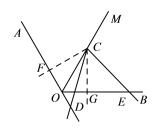
∴∠OFC=∠OGC=90°,
∵∠AOB=120°,
∴∠FCG=60°,
同(1)的方法得,OF=![]() OC,OG=
OC,OG=![]() OC,
OC,
∴OF+OG=OC,
∵CF⊥OA,CG⊥OB,且点C是∠AOB的平分线OM上一点,
∴CF=CG,
∵∠DCE=60°,∠FCG=60°,
∴∠DCF=∠ECG,
∴△CFD≌△CGE,
∴DF=EG,
∴OF=DF﹣OD=EG﹣OD,
OG=OE﹣EG,
∴OF+OG=EG﹣OD+OE﹣EG=OE﹣OD,
∴OE﹣OD=OC.


科目:初中数学 来源: 题型:
【题目】如图,一艘船由A港沿北偏东60°方向航行10km至B港,然后再沿北偏西30°方向航行10km至C港.
(1)求A,C两港之间的距离(结果保留到0.1km,参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732);
≈1.732);
(2)确定C港在A港的什么方向.

查看答案和解析>>
科目:初中数学 来源: 题型:
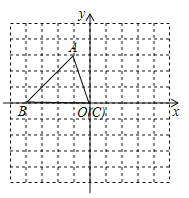
【题目】(2016黑龙江省齐齐哈尔市)如图,平面直角坐标系内,小正方形网格的边长为1个单位长度,△ABC的三个顶点的坐标分别为A(﹣1,3),B(﹣4,0),C(0,0)
(1)画出将△ABC向上平移1个单位长度,再向右平移5个单位长度后得到的△A1B1C1;
(2)画出将△ABC绕原点O顺时针方向旋转90°得到△A2B2O;
(3)在x轴上存在一点P,满足点P到A1与点A2距离之和最小,请直接写出P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
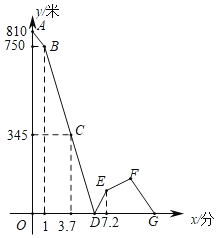
【题目】已知甲乙两地之间的距离为810米,小明和小天分别从甲乙两地出发,匀速相向而行,已知小明先出发1分钟后,小天再出发,两人在甲乙之间的丙地相遇,此时,小明发现有小学同学也在丙地,于是聊了一会儿,随后以原来速度的![]() 倍返回甲地,小天相遇后继续以原速向甲地前行,到达甲地后立即原速返回,直至再次与小明相遇.已知在整个过程中,小明、小天两人之间的距离
倍返回甲地,小天相遇后继续以原速向甲地前行,到达甲地后立即原速返回,直至再次与小明相遇.已知在整个过程中,小明、小天两人之间的距离![]() (米与小明出发的时间
(米与小明出发的时间![]() (分钟)之间的关系如图所示,则在第二次相遇时两人距离乙地______米.
(分钟)之间的关系如图所示,则在第二次相遇时两人距离乙地______米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究函数![]() 的图象和性质.洋洋同学根据学习函数的经验,对函数
的图象和性质.洋洋同学根据学习函数的经验,对函数![]() 的图象和性质进行了探究,下面是洋洋的探究过程,请补充完成:
的图象和性质进行了探究,下面是洋洋的探究过程,请补充完成:
(1)化简函数解析式:当![]() 时,
时,![]() ______,当
______,当![]() 时,
时,![]() ______;
______;
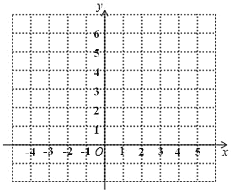
(2)根据(1)的结果,请在所给坐标系中画出函数![]() 的图象;(直尺画图,不用列表)
的图象;(直尺画图,不用列表)
(3)观察函数图象,请写出该函数的一条性质:______.
查看答案和解析>>
科目:初中数学 来源: 题型:
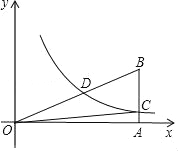
【题目】若关于x的一元二次方程x2+(2k﹣1)x+k2=0的两根a、b满足a2﹣b2=0,双曲线![]() (x>0)经过Rt△OAB斜边OB的中点D,与直角边AB交于C(如图),则S△OBC为( )
(x>0)经过Rt△OAB斜边OB的中点D,与直角边AB交于C(如图),则S△OBC为( )
A. 3 B. ![]() C. 6 D. 3或
C. 6 D. 3或![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列不是一次函数关系的是( )
A.矩形一条边的长固定,面积与另一条边的长的关系
B.矩形一条边的长固定,周长与另一条边的长的关系
C.圆的周长与直径的关系
D.圆的面积与直径的关系
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班“数学兴趣小组”对函数y=![]() +x的图象与性质进行了探究,探究过程如下,请补充完整.
+x的图象与性质进行了探究,探究过程如下,请补充完整.
(1)函数y=![]() +x的自变量x的取值范围是 ;
+x的自变量x的取值范围是 ;
(2)下表是y与x的几组对应值.
x | … | ﹣3 | ﹣2 | ﹣1 | 0 |
|
|
|
| 2 | 3 | 4 | 5 | … |
y | … | ﹣ | ﹣ | ﹣ | ﹣1 | ﹣ | ﹣ |
|
| 3 |
| m |
| … |
求m的值;
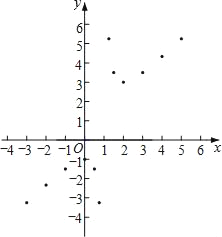
(3)如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点,根据描出的点,画出该函数的图象;
(4)进一步探究发现,该函数图象在第一象限内的最低点的坐标是(2,3),结合函数的图象,写出该函数的其它性质(一条即可): .
(5)小明发现,①该函数的图象关于点( , )成中心对称;
②该函数的图象与一条垂直于x轴的直线无交点,则这条直线为 ;
③直线y=m与该函数的图象无交点,则m的取值范围为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
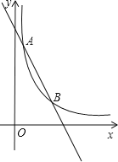
【题目】如图,已知反比例函数![]() 的图象与一次函数y=kx+b的图象交于点A(1,m),B (n,2)两点
的图象与一次函数y=kx+b的图象交于点A(1,m),B (n,2)两点
(1)求一次函数的解析式;
(2)直接写出不等式![]() ≥kx+b的解集;
≥kx+b的解集;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com