
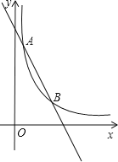
【题目】如图,已知反比例函数![]() 的图象与一次函数y=kx+b的图象交于点A(1,m),B (n,2)两点
的图象与一次函数y=kx+b的图象交于点A(1,m),B (n,2)两点
(1)求一次函数的解析式;
(2)直接写出不等式![]() ≥kx+b的解集;
≥kx+b的解集;
 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
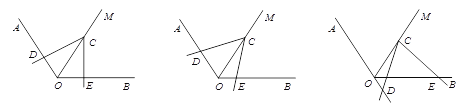
【题目】如图,已知∠AOB=120°,在∠AOB的平分线OM上有一点C,将一个60°角的顶点与点C重合,它的两条边分别与直线OA、OB相交于点D、E.
(1)当∠DCE绕点C旋转到CD与OA垂直时(如图1),请猜想OE+OD与OC的数量关系,并说明理由;
(2)当∠DCE绕点C旋转到CD与OA不垂直时,到达图2的位置,(1)中的结论是否成立?并说明理由;
(3)当∠DCE绕点C旋转到CD与OA的反向延长线相交时,上述结论是否成立?若成立,请给于证明;若不成立,线段OD、OE与OC之间又有怎样的数量关系?请写出你的猜想,不需证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某中学学生对“厉行勤俭节约,反对铺张浪费”主题活动的参与情况,小强在全校范围内随机抽取了若干名学生并就某日午饭浪费饭菜情况进行了调查,将调查内容分为四组:![]() 饭和菜全部吃完;
饭和菜全部吃完;![]() :有剩饭但菜吃完;
:有剩饭但菜吃完;![]() :饭吃完但菜有剩;
:饭吃完但菜有剩;![]() :饭和菜都有剩.根据调查结果,绘制了如图所示两幅不完整的统计图.
:饭和菜都有剩.根据调查结果,绘制了如图所示两幅不完整的统计图.

回答下列问题:
(1)这次被抽查的学生共有 人,扇形统计图中,“![]() 组”所对应的圆心角的度数为 ;
组”所对应的圆心角的度数为 ;
(2)补全条形统计图;
(3)已知该中学共有学生![]() 人,请估计这日午饭有剩饭的学生人数,若按平均每人剩
人,请估计这日午饭有剩饭的学生人数,若按平均每人剩![]() 克米饭计算,这日午饭将浪费多少千克米饭?
克米饭计算,这日午饭将浪费多少千克米饭?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,抛物线
,抛物线![]() 的对称轴是
的对称轴是![]() 且经过
且经过![]() 、
、![]() 两点,与
两点,与![]() 轴的另一交点为点
轴的另一交点为点![]() ,连结
,连结![]() .
.
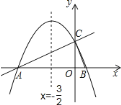
(1)填空:点![]() 、点
、点![]() 和点
和点![]() 的坐标分别为
的坐标分别为![]() ________,
________,![]() ________,
________,![]() ________;
________;
(2)求证:![]() ;
;
(3)求抛物线解析式;
(4)若点![]() 为直线
为直线![]() 上方的抛物线上的一点,连结
上方的抛物线上的一点,连结![]() ,
,![]() ,求
,求![]() 面积的最大值,并求出此时点
面积的最大值,并求出此时点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是根据九年级某班50名同学一周的锻炼情况绘制的条形统计图,下面关于该班50名同学一周锻炼时间的说法错误的是( )

A.平均数是6
B.中位数是6.5
C.众数是7
D.平均每周锻炼超过6小时的人数占该班人数的一半
查看答案和解析>>
科目:初中数学 来源: 题型:
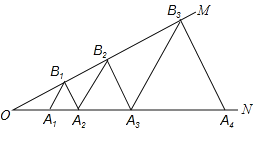
【题目】如图,∠MON=30°,点A1、A2、A3、……在射线ON上,点B1、B2、B3、……在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4,……均为等边三角形,若OA1=1,则△A2019B2019A2020的边长为__________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,⊙C的半径为r,P是与圆心C不重合的点,点P关于⊙C的反称点的定义如下:若在射线CP上存在一点P′,满足CP+CP′=2r,则称P′为点P关于⊙C的反称点,如图为点P及其关于⊙C的反称点P′的示意图.
特别地,当点P′与圆心C重合时,规定CP′=0.
(1)当⊙O的半径为1时.
①分别判断点M(2,1),N(![]() ,0),T(1,
,0),T(1, ![]() )关于⊙O的反称点是否存在?若存在,求其坐标;
)关于⊙O的反称点是否存在?若存在,求其坐标;
②点P在直线y=﹣x+2上,若点P关于⊙O的反称点P′存在,且点P′不在x轴上,求点P的横坐标的取值范围;
(2)⊙C的圆心在x轴上,半径为1,直线y=﹣![]() x+2
x+2![]() 与x轴、y轴分别交于点A,B,若线段AB上存在点P,使得点P关于⊙C的反称点P′在⊙C的内部,求圆心C的横坐标的取值范围.
与x轴、y轴分别交于点A,B,若线段AB上存在点P,使得点P关于⊙C的反称点P′在⊙C的内部,求圆心C的横坐标的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近年来,共享单车逐渐成为高校学生喜爱的“绿色出行”方式之一,自2016年国庆后,许多高校均投放了使用手机支付就可随取随用的共享单车.某高校为了解本校学生出行使用共享单车的情况,随机调查了某天部分出行学生使用共享单车的情况,并整理成如下统计表.
使用次数 | 0 | 1 | 2 | 3 | 4 | 5 |
人数 | 11 | 15 | 23 | 28 | 18 | 5 |
(1)这天部分出行学生使用共享单车次数的中位数是 ,众数是 ,该中位数的意义是 ;
(2)这天部分出行学生平均每人使用共享单车约多少次?(结果保留整数)
(3)若该校某天有1500名学生出行,请你估计这天使用共享单车次数在3次以上(含3次)的学生有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com