
°æƒø°øƒ≥∞ý°∞ ˝—ß–À»§–°◊È°±∂‘∫Ø ˝y£Ω![]() +xµƒÕºœÛ”Ζ‘÷ Ω¯––¡ÀÃΩæø£¨ÃΩæøπ˝≥ûÁœ¬£¨«Î≤π≥‰ÕÍ’˚£Æ
+xµƒÕºœÛ”Ζ‘÷ Ω¯––¡ÀÃΩæø£¨ÃΩæøπ˝≥ûÁœ¬£¨«Î≤π≥‰ÕÍ’˚£Æ
(1)∫Ø ˝y£Ω![]() +xµƒ◊‘±‰¡øxµƒ»°÷µ∑∂Œß «°° °°£ª
+xµƒ◊‘±‰¡øxµƒ»°÷µ∑∂Œß «°° °°£ª
(2)œ¬±Ì «y”Îxµƒº∏◊È∂‘”¶÷µ£Æ
x | °≠ | ©Å3 | ©Å2 | ©Å1 | 0 |
|
|
|
| 2 | 3 | 4 | 5 | °≠ |
y | °≠ | ©Å | ©Å | ©Å | ©Å1 | ©Å | ©Å |
|
| 3 |
| m |
| °≠ |
«Ûmµƒ÷µ£ª
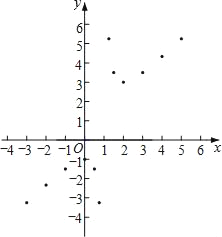
(3)»ÁÕº£¨‘⁄∆Ω√Ê÷±Ω«◊¯±ÍœµxOy÷–£¨√Ë≥ˆ¡À“‘…œ±Ì÷–∏˜∂‘∂‘”¶÷µŒ™◊¯±Íµƒµ„£¨∏˘æð√Ë≥ˆµƒµ„£¨ª≠≥ˆ∏√∫Ø ˝µƒÕºœÛ£ª
(4)Ω¯“ª≤ΩÃΩæø∑¢œ÷£¨∏√∫Ø ˝ÕºœÛ‘⁄µ⁄“ªœÛœÞƒ⁄µƒ◊ÓµÕµ„µƒ◊¯±Í «(2£¨3)£¨Ω·∫œ∫Ø ˝µƒÕºœÛ£¨–¥≥ˆ∏√∫Ø ˝µƒ∆‰À¸–‘÷ (“ªÃıº¥ø…)£∫°° °°£Æ
(5)–°√˜∑¢œ÷£¨¢Ÿ∏√∫Ø ˝µƒÕºœÛπÿ”⁄µ„(°° °°£¨°° °°)≥…÷––ƒ∂‘≥∆£ª
¢⁄∏√∫Ø ˝µƒÕºœÛ”ΓªÃı¥π÷±”⁄x÷·µƒ÷±œþŒÞΩªµ„£¨‘Ú’‚Ãı÷±œþŒ™°° °°£ª
¢€÷±œþy£Ωm”Î∏√∫Ø ˝µƒÕºœÛŒÞΩªµ„£¨‘Úmµƒ»°÷µ∑∂ŒßŒ™°° °°£Æ
°æ¥∞∏°ø(1)x°Ÿ1,(2)![]() ,(4)x£æ2 ±yÀÊxµƒ‘ˆ¥Û∂¯‘ˆ¥Û,
,(4)x£æ2 ±yÀÊxµƒ‘ˆ¥Û∂¯‘ˆ¥Û,
(5)¢Ÿ( ![]() £¨
£¨![]() )£¨¢⁄x=1£¨¢€©Å1£ºm£º3.
)£¨¢⁄x=1£¨¢€©Å1£ºm£º3.
°æΩ‚Œˆ°ø
£®1£©¡Ó∑÷ƒ∏≤ªµ»”⁄¡„º¥ø…«Û≥ˆ±‰¡øxµƒ»°÷µ∑∂Œß£ª
£®2£©∞—x=4¥˙»Îy=![]() +xº¥ø…«Û≥ˆmµƒ÷µ£ª
+xº¥ø…«Û≥ˆmµƒ÷µ£ª
£®3£©”√π‚ª¨«˙œþ∞—∏˜µ„À≥¥Œ¡¨Ω”º¥ø…£ª
£®4£©∏˘æðÕºœÒΩ‚¥º¥ø…£¨»Áx£æ2 ±yÀÊxµƒ‘ˆ¥Û∂¯‘ˆ¥Û£Æ£®¥∞∏≤ªŒ®“ª£©£ª
£®5£©∏˘æðÕºœÒΩ‚¥º¥ø….
£®1£©∫Ø ˝y=![]() +xµƒ◊‘±‰¡øxµƒ»°÷µ∑∂Œß «x°Ÿ1£Æ
+xµƒ◊‘±‰¡øxµƒ»°÷µ∑∂Œß «x°Ÿ1£Æ
π ¥∞∏Œ™x°Ÿ1£Æ
£®2£©x=4 ±£¨y=![]() £¨
£¨
°ým=![]() £Æ
£Æ
£®3£©∫Ø ˝ÕºœÛ»ÁÕºÀ˘ æ£∫
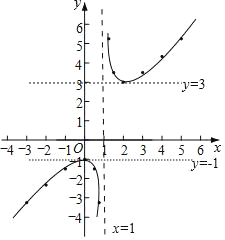
£®4£©x£æ2 ±yÀÊxµƒ‘ˆ¥Û∂¯‘ˆ¥Û£Æ£®¥∞∏≤ªŒ®“ª£©
π ¥∞∏Œ™£∫x£æ2 ±yÀÊxµƒ‘ˆ¥Û∂¯‘ˆ¥Û£Æ
£®5£©¢Ÿ∏√∫Ø ˝µƒÕºœÛπÿ”⁄µ„£®1£¨1£©≥…÷––ƒ∂‘≥∆£ª
¢⁄∏√∫Ø ˝µƒÕºœÛ”ΓªÃı¥π÷±”⁄x÷·µƒ÷±œþŒÞΩªµ„£¨‘Ú’‚Ãı÷±œþŒ™x=1£ª
¢€÷±œþy=m”Î∏√∫Ø ˝µƒÕºœÛŒÞΩªµ„£¨‘Úmµƒ»°÷µ∑∂ŒßŒ™©Å1£ºm£º3£ª
π ¥∞∏Œ™1£¨1£¨x=1£¨©Å1£ºm£º3£ª



| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨ «∂˛¥Œ∫Ø ˝y=ax2+bx+c£®a°Ÿ0£©µƒÕºœÛµƒ“ª≤ø∑÷£¨∏¯≥ˆœ¬¡–√¸Ã‚£∫¢Ÿabc£º0£ª¢⁄ 2a£æb£ª¢€b=a+c£ª¢Ð8a+c£æ0£ª¢ðax2+bx+c=0µƒ¡Ω∏˘∑÷±Œ™©Å3∫Õ1£Æ∆‰÷–’˝»∑µƒ√¸Ã‚”–£® £©

A. 2∏ˆ B. 3∏ˆ C. 4∏ˆ D. 5∏ˆ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
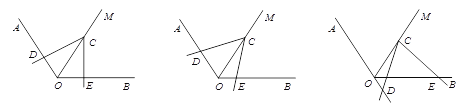
°æƒø°ø»ÁÕº£¨“—÷™°œAOB=120°„£¨‘⁄°œAOBµƒ∆Ω∑÷œþOM…œ”–“ªµ„C£¨Ω´“ª∏ˆ60°„Ω«µƒ∂•µ„”ε„C÷ÿ∫œ£¨À¸µƒ¡ΩÃı±þ∑÷±”Î÷±œþOA°¢OBœýΩª”⁄µ„D°¢E£Æ
£®1£©µ±°œDCE»∆µ„C–˝◊™µΩCD”ÎOA¥π÷± ±£®»ÁÕº1£©£¨«Î≤¬œÎOE+OD”ÎOCµƒ ˝¡øπÿœµ£¨≤¢Àµ√˜¿Ì”…£ª
£®2£©µ±°œDCE»∆µ„C–˝◊™µΩCD”ÎOA≤ª¥π÷± ±£¨µΩ¥ÔÕº2µƒŒª÷√£¨£®1£©÷–µƒΩ·¬€ «∑Ò≥…¡¢£ø≤¢Àµ√˜¿Ì”…£ª
£®3£©µ±°œDCE»∆µ„C–˝◊™µΩCD”ÎOAµƒ∑¥œÚ—”≥§œþœýΩª ±£¨…œ ˆΩ·¬€ «∑Ò≥…¡¢£ø»Ù≥…¡¢£¨«Î∏¯”⁄÷§√˜£ª»Ù≤ª≥…¡¢£¨œþ∂ŒOD°¢OE”ÎOC÷ƺ‰”÷”–‘ı—˘µƒ ˝¡øπÿœµ£ø«Î–¥≥ˆƒ„µƒ≤¬œÎ£¨≤ª–Ë÷§√˜£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
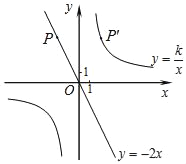
°æƒø°ø»ÁÕº£¨“—÷™÷±œþy£Ω©Å2xæ≠π˝µ„P£®©Å2£¨a£©£¨µ„Pπÿ”⁄y÷·µƒ∂‘≥∆µ„P°‰‘⁄∑¥±»¿˝∫Ø ˝y£Ω![]() £®k°Ÿ0£©µƒÕºœÛ…œ£Æ
£®k°Ÿ0£©µƒÕºœÛ…œ£Æ
£®1£©«Û∑¥±»¿˝∫Ø ˝µƒΩ‚Œˆ Ω£ª
£®2£©÷±Ω”–¥≥ˆµ±y£º4 ±xµƒ»°÷µ∑∂Œß£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
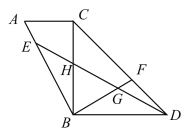
°æƒø°ø»ÁÕº£¨![]() ÷–£¨
÷–£¨![]() £¨
£¨![]() £¨
£¨![]() £¨‘⁄
£¨‘⁄![]() …œΩÿ»°
…œΩÿ»°![]() £¨ π
£¨ π![]() £¨π˝µ„
£¨π˝µ„![]() ◊˜
◊˜![]() µƒ¥πœþ£¨Ωª
µƒ¥πœþ£¨Ωª![]() ”⁄µ„
”⁄µ„![]() £¨¡¨Ω”
£¨¡¨Ω”![]() £¨Ωª
£¨Ωª![]() ”⁄µ„
”⁄µ„![]() £¨Ωª
£¨Ωª![]() ”⁄µ„
”⁄µ„![]() £¨
£¨![]() £¨‘Ú
£¨‘Ú![]() ____________.
____________.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øŒ™¡À≤Œº”°∞æ£÷ð –÷––°—ß…˙ ◊ΩÏ ´¥ ¥Ûª·°±£¨ƒ≥–£∞ÀƒÍº∂µƒ¡Ω∞ý—ß…˙Ω¯––¡À‘§—°£¨∆‰÷–∞ý…œ«∞5√˚—ß…˙µƒ≥…º®£®∞Ÿ∑÷÷∆£©∑÷±Œ™£∫∞À£®1£©∞ý86£¨85£¨77£¨92£¨85£ª∞À£®2£©∞ý79£¨85£¨92£¨85£¨89£ÆÕ®π˝ ˝æð∑÷Œˆ£¨¡–±Ì»Áœ¬£∫
∞ýº∂ | ∆Ωæ˘∑÷ | ÷–Œª ˝ | ÷⁄ ˝ | ∑Ω≤Ó |
∞À£®1£© | 85 | b | c | 22.8 |
∞À£®2£© | a | 85 | 85 | 19.2 |
£®1£©÷±Ω”–¥≥ˆ±Ì÷–a£¨b£¨cµƒ÷µ£ª
£®2£©∏˘æð“‘…œ ˝æð∑÷Œˆ£¨ƒ„»œŒ™ƒƒ∏ˆ∞ý«∞5√˚Õ¨—ßµƒ≥…º®Ωœ∫√£øÀµ√˜¿Ì”…£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øŒ™¡ÀΩ‚ƒ≥÷–—ß—ß…˙∂‘°∞¿˜––«⁄ºÛΩ⁄‘º£¨∑¥∂‘∆Ã’≈¿À∑—°±÷˜Ã‚ªÓ∂صƒ≤Œ”ΫÈøˆ£¨–°«ø‘⁄»´–£∑∂Œßƒ⁄Àʪ˙≥È»°¡À»Ù∏…√˚—ß…˙≤¢æÕƒ≥»’ŒÁ∑π¿À∑—∑π≤À«ÈøˆΩ¯––¡Àµ˜≤È£¨Ω´µ˜≤ȃ⁄»ð∑÷Œ™Àƒ◊È£∫![]() ∑π∫Õ≤À»´≤ø≥‘ÕÍ£ª
∑π∫Õ≤À»´≤ø≥‘ÕÍ£ª![]() £∫”– £∑πµ´≤À≥‘ÕÍ£ª
£∫”– £∑πµ´≤À≥‘ÕÍ£ª![]() £∫∑π≥‘Õ͵´≤À”– ££ª
£∫∑π≥‘Õ͵´≤À”– ££ª![]() £∫∑π∫Õ≤À∂º”– £.∏˘æðµ˜≤ÈΩ·π˚£¨ªÊ÷∆¡À»ÁÕºÀ˘ æ¡Ω∑˘≤ªÕÍ’˚µƒÕ≥º∆Õº.
£∫∑π∫Õ≤À∂º”– £.∏˘æðµ˜≤ÈΩ·π˚£¨ªÊ÷∆¡À»ÁÕºÀ˘ æ¡Ω∑˘≤ªÕÍ’˚µƒÕ≥º∆Õº.

ªÿ¥œ¬¡–Œ £∫
£®1£©’‚¥Œ±ª≥È≤ȵƒ—ß…˙π≤”– »À£¨…»–ŒÕ≥º∆Õº÷–£¨°∞![]() ◊È°±À˘∂‘”¶µƒ‘≤–ƒΩ«µƒ∂» ˝Œ™ £ª
◊È°±À˘∂‘”¶µƒ‘≤–ƒΩ«µƒ∂» ˝Œ™ £ª
£®2£©≤π»´Ãı–ŒÕ≥º∆Õº£ª
£®3£©“—÷™∏√÷–—ßπ≤”–—ß…˙![]() »À£¨«Îπ¿º∆’‚»’ŒÁ∑π”– £∑πµƒ—ß…˙»À ˝£¨»Ù∞¥∆Ωæ˘√ø»À £
»À£¨«Îπ¿º∆’‚»’ŒÁ∑π”– £∑πµƒ—ß…˙»À ˝£¨»Ù∞¥∆Ωæ˘√ø»À £![]() øÀ√◊∑πº∆À„£¨’‚»’ŒÁ∑πΩ´¿À∑—∂ý…Ÿ«ßøÀ√◊∑π£ø
øÀ√◊∑πº∆À„£¨’‚»’ŒÁ∑πΩ´¿À∑—∂ý…Ÿ«ßøÀ√◊∑π£ø
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨‘⁄∆Ω√Ê÷±Ω«◊¯±Íœµ÷–£¨÷±œþ![]() ”Î
”Î![]() ÷·Ωª”⁄µ„
÷·Ωª”⁄µ„![]() £¨”Î
£¨”Î![]() ÷·Ωª”⁄µ„
÷·Ωª”⁄µ„![]() £¨≈◊ŒÔœþ
£¨≈◊ŒÔœþ![]() µƒ∂‘≥∆÷· «
µƒ∂‘≥∆÷· «![]() «“æ≠π˝
«“æ≠π˝![]() °¢
°¢![]() ¡Ωµ„£¨”Î
¡Ωµ„£¨”Î![]() ÷·µƒ¡Ì“ªΩªµ„Œ™µ„
÷·µƒ¡Ì“ªΩªµ„Œ™µ„![]() £¨¡¨Ω·
£¨¡¨Ω·![]() £Æ
£Æ
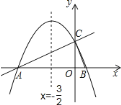
£®1£©ÃÓø’£∫µ„![]() °¢µ„
°¢µ„![]() ∫Õµ„
∫Õµ„![]() µƒ◊¯±Í∑÷±Œ™
µƒ◊¯±Í∑÷±Œ™![]() ________£¨
________£¨![]() ________£¨
________£¨![]() ________£ª
________£ª
£®2£©«Û÷§£∫![]() £ª
£ª
£®3£©«Û≈◊ŒÔœþΩ‚Œˆ Ω£ª
£®4£©»Ùµ„![]() Œ™÷±œþ
Œ™÷±œþ![]() …œ∑Ωµƒ≈◊ŒÔœþ…œµƒ“ªµ„£¨¡¨Ω·
…œ∑Ωµƒ≈◊ŒÔœþ…œµƒ“ªµ„£¨¡¨Ω·![]() £¨
£¨![]() £¨«Û
£¨«Û![]() √ʪ˝µƒ◊Ó¥Û÷µ£¨≤¢«Û≥ˆ¥À ±µ„
√ʪ˝µƒ◊Ó¥Û÷µ£¨≤¢«Û≥ˆ¥À ±µ„![]() µƒ◊¯±Í£Æ
µƒ◊¯±Í£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø‘⁄∆Ω√Ê÷±Ω«◊¯±ÍœµxOy÷–£¨°—Cµƒ∞Îæ∂Œ™r£¨P «”Α≤–ƒC≤ª÷ÿ∫œµƒµ„£¨µ„Pπÿ”⁄°—Cµƒ∑¥≥∆µ„µƒ∂®“»Áœ¬£∫»Ù‘⁄…‰œþCP…œ¥Ê‘⁄“ªµ„P°‰£¨¬˙◊„CP+CP°‰=2r£¨‘Ú≥∆P°‰Œ™µ„Pπÿ”⁄°—Cµƒ∑¥≥∆µ„£¨»ÁÕºŒ™µ„Pº∞∆‰πÿ”⁄°—Cµƒ∑¥≥∆µ„P°‰µƒ æ“‚Õº£Æ
Ãÿ±µÿ£¨µ±µ„P°‰”Α≤–ƒC÷ÿ∫œ ±£¨πÊ∂®CP°‰=0£Æ
£®1£©µ±°—Oµƒ∞Îæ∂Œ™1 ±£Æ
¢Ÿ∑÷±≈–∂œµ„M£®2£¨1£©£¨N£®![]() £¨0£©£¨T£®1£¨
£¨0£©£¨T£®1£¨ ![]() £©πÿ”⁄°—Oµƒ∑¥≥∆µ„ «∑ҥʑ⁄£ø»Ù¥Ê‘⁄£¨«Û∆‰◊¯±Í£ª
£©πÿ”⁄°—Oµƒ∑¥≥∆µ„ «∑ҥʑ⁄£ø»Ù¥Ê‘⁄£¨«Û∆‰◊¯±Í£ª
¢⁄µ„P‘⁄÷±œþy=©Åx+2…œ£¨»Ùµ„Pπÿ”⁄°—Oµƒ∑¥≥∆µ„P°‰¥Ê‘⁄£¨«“µ„P°‰≤ª‘⁄x÷·…œ£¨«Ûµ„Pµƒ∫·◊¯±Íµƒ»°÷µ∑∂Œß£ª
£®2£©°—Cµƒ‘≤–ƒ‘⁄x÷·…œ£¨∞Îæ∂Œ™1£¨÷±œþy=©Å![]() x+2
x+2![]() ”Îx÷·°¢y÷·∑÷±Ωª”⁄µ„A£¨B£¨»Ùœþ∂ŒAB…œ¥Ê‘⁄µ„P£¨ πµ√µ„Pπÿ”⁄°—Cµƒ∑¥≥∆µ„P°‰‘⁄°—Cµƒƒ⁄≤ø£¨«Û‘≤–ƒCµƒ∫·◊¯±Íµƒ»°÷µ∑∂Œß£Æ
”Îx÷·°¢y÷·∑÷±Ωª”⁄µ„A£¨B£¨»Ùœþ∂ŒAB…œ¥Ê‘⁄µ„P£¨ πµ√µ„Pπÿ”⁄°—Cµƒ∑¥≥∆µ„P°‰‘⁄°—Cµƒƒ⁄≤ø£¨«Û‘≤–ƒCµƒ∫·◊¯±Íµƒ»°÷µ∑∂Œß£Æ

≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
π˙º —ß–£”≈—° - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com