
分析 两个数相减,然后根据减去一个数等于加上这个数的相反数进行计算即可得解;再根据两点间的距离与差的关系解答.
解答 解:a=2,b=6时,a-b=2-6=-4,
|-4|=4,
所以,A、B间的距离为4;
a=0,b=6时,a-b=0-6=-6,
|-6|=6,
所以,A、B间的距离为6;
a=2,b=-6时,a-b=2-(-6)=2+6=8,
|8|=8,
所以,A、B间的距离为8;
a=-2,b=-6时,a-b=-2-(-6)=-2+6=4,
|4|=4,
所以,A、B间的距离为4.
总结:点A,B之间的距离等于数a,b的差的绝对值.
点评 本题考查了有理数的减法,数轴,主要是数轴上两点间的距离的求解方法的推理,是基础题,需熟记.


科目:初中数学 来源: 题型:选择题
 一条进村公路修到湖边时需拐弯绕湖而过,如图,如果第一次拐弯∠A=100°,第二次拐弯∠B=160°,第三次拐弯的角是∠C,要使第三次拐弯后道路恰好与第一次拐弯之前道路平行,则∠C度数是( )
一条进村公路修到湖边时需拐弯绕湖而过,如图,如果第一次拐弯∠A=100°,第二次拐弯∠B=160°,第三次拐弯的角是∠C,要使第三次拐弯后道路恰好与第一次拐弯之前道路平行,则∠C度数是( )| A. | 110° | B. | 120° | C. | 135° | D. | 155° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
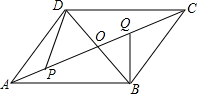 ?ABCD的对角线AC,BD交于点O,∠AOD=60°,∠ADO=90°,BD=12,点P是AO上一动点,点Q是OC上一动点(P,Q不与端点重合),且AP=OQ,连接BQ,DP.
?ABCD的对角线AC,BD交于点O,∠AOD=60°,∠ADO=90°,BD=12,点P是AO上一动点,点Q是OC上一动点(P,Q不与端点重合),且AP=OQ,连接BQ,DP.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com