
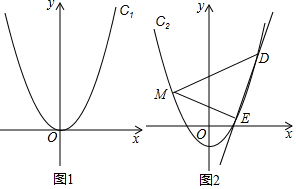
���� ��1���ѵ��������������߽���ʽ�����a��ֵ�������������߽���ʽ��������䶥������ͶԳ��
��2����ֱ��l����ʽ�����P�����꣬��A��x1��y1����B��x2��y2������PA=AB������ֱ�ߺ������߽���ʽ�������A�����ꣻ
��3������M��ֱ��l��x�ᣬ����D��DF��l��F������E��EG��l��G����D��x1��x12-h����E��x2��x22-h���������������ε����ʿ����x1+x2=4����ֱ��DE����ʽΪy=kx+b����D��E�����������k=x1+x2=4����֤�ý��ۣ�
��� �⣺
��1����������C1��y=ax2������-1��1����
��a=1��
�������߽���ʽΪy=x2��
�ඥ������Ϊ��0��0�����Գ���Ϊy�ᣬ
�ʴ�Ϊ��y=x2����0��0�����Գ���Ϊy�
��2���ߵ�x=-2ʱ��y=-2��
��P��-2��-2����
��A��x1��y1����B��x2��y2��
��PA=PB
��-2+x2=2x1��
����$\left\{\begin{array}{l}y=kx+2k-2\\ y={x^2}\end{array}\right.$��������x2-kx-2k+2=0
��x1+x2=k �ڣ�x1x2=-2k+2 ��
�ɢٵã�${x_1}=\frac{k-2}{3}$������ڢ۵ã�$k=-4��3\sqrt{3}$��
��A��������$\sqrt{3}-2$��$7-4\sqrt{3}$����$-\sqrt{3}-2$��$7+4\sqrt{3}$����
��3������M��ֱ��l��x�ᣬ����D��DF��l��F������E��EG��l��G��
��D��x1��x12-h����E��x2��x22-h�������MDF�ס�MEG��
��$\frac{{��{x_1}^2-h��-��4-h��}}{{{x_1}+2}}=\frac{{-[��{x_2}^2-h��-��4-h��]}}{{{x_2}+2}}$����x1+x2=4��
��ֱ��DE�Ľ���ʽΪy=kx+b
��$\left\{\begin{array}{l}k{x_1}+b={x_1}^2-h\\ k{x_2}+b={x_2}^2-h\end{array}\right.$����k=x1+x2=4
��ֱ��DEһ�����ԭ���ֱ��y=4xƽ�У�
���� ����Ϊ���κ������ۺ�Ӧ�ã��漰����ϵ����������ͼ��Ľ��㡢һԪ���η��̸���ϵ���Ĺ�ϵ����ֱ��ƽ�С����������ε����ʵ�֪ʶ���ڣ�1����ע�����ϵ������Ӧ�ò��裬�ڣ�2���и��ݺ���ͼ��Ľ��������õ�x1��x2��k�Ĺ�ϵ�ǽ���Ĺؼ����ڣ�3����D��E�������ʾ��k�ǽ���Ĺؼ������⿼��֪ʶ��϶࣬�ۺ��Խ�ǿ���ѶȽϴ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
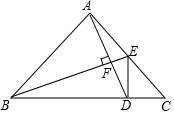 ��ͼ����Rt��ABC�У���BAC=90�㣬AB=AC����ABC=��ACB��D��E�ֱ���BC��AC�ϵĵ㣬��AD��BE����ADB=��CDE��CE=2����S��ADE=$\frac{4}{3}$��
��ͼ����Rt��ABC�У���BAC=90�㣬AB=AC����ABC=��ACB��D��E�ֱ���BC��AC�ϵĵ㣬��AD��BE����ADB=��CDE��CE=2����S��ADE=$\frac{4}{3}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{4}$ | B�� | $\frac{1}{12}$ | C�� | $\frac{1}{13}$ | D�� | $\frac{1}{52}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
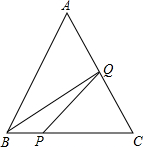 �ڡ�ABC�У���֪AB=BC=CA=4cm����P��Q�ֱ��B��C����ͬʱ���������е�P��BC���յ�C�˶����ٶ�Ϊ1cm/s����Q��CA��AB���յ�B�˶����ٶ�Ϊ2cm/s���������˶���ʱ��Ϊx��s������x=2��$\frac{16}{5}$����BPQ��ֱ�������Σ�
�ڡ�ABC�У���֪AB=BC=CA=4cm����P��Q�ֱ��B��C����ͬʱ���������е�P��BC���յ�C�˶����ٶ�Ϊ1cm/s����Q��CA��AB���յ�B�˶����ٶ�Ϊ2cm/s���������˶���ʱ��Ϊx��s������x=2��$\frac{16}{5}$����BPQ��ֱ�������Σ��鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com