
【题目】如图,在平面直角坐标系中,抛物线y=ax2+2x+c与x轴交于A(﹣1,0)B(3,0)两点,与y轴交于点C.
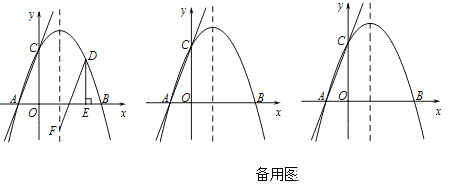
(1)求抛物线y=ax2+2x+c的解析式:;
(2)点D为抛物线上对称轴右侧、x轴上方一点,DE⊥x轴于点E,DF∥AC交抛物线对称轴于点F,求DE+DF的最大值;
(3)①在拋物线上是否存在点P,使以点A,P,C为顶点,AC为直角边的三角形是直角三角形?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由;
②点Q在抛物线对称轴上,其纵坐标为t,请直接写出△ACQ为锐角三角形时t的取值范围.
【答案】(1)y=﹣x2+2x+3;(2)DE+DF有最大值为![]() ;(3)①存在,P的坐标为(
;(3)①存在,P的坐标为(![]() ,
,![]() )或(
)或(![]() ,
,![]() );②
);②![]() <t<
<t<![]() .
.
【解析】
(1)设抛物线解析式为y=a(x+1)(x﹣3),根据系数的关系,即可解答
(2)先求出当x=0时,C的坐标,设直线AC的解析式为y=px+q,把A,C的坐标代入即可求出AC的解析式,过D作DG垂直抛物线对称轴于点G,设D(x,﹣x2+2x+3),得出DE+DF=﹣x2+2x+3+![]() (x-1)=﹣x2+(2+
(x-1)=﹣x2+(2+![]() )x+3-
)x+3-![]() ,即可解答
,即可解答
(3)①过点C作AC的垂线交抛物线于另一点P1,求出直线PC的解析式,再结合抛物线的解析式可求出P1,过点A作AC的垂线交抛物线于另一点P2,再利用A的坐标求出P2,即可解答
②观察函数图象与△ACQ为锐角三角形时的情况,即可解答
解:(1)设抛物线解析式为y=a(x+1)(x﹣3),即y=ax2﹣2ax﹣3a,
∴﹣2a=2,解得a=﹣1,
∴抛物线解析式为y=﹣x2+2x+3;
(2)当x=0时,y=﹣x2+2x+3=3,则C(0,3),设直线AC的解析式为y=px+q,把A(﹣1,0),C(0,3)代入得![]() ,解得
,解得![]() ,∴直线AC的解析式为y=3x+3,如答图1,过D作DG垂直抛物线对称轴于点G,设D(x,﹣x2+2x+3),
,∴直线AC的解析式为y=3x+3,如答图1,过D作DG垂直抛物线对称轴于点G,设D(x,﹣x2+2x+3),
∵DF∥AC,
∴∠DFG=∠ACO,易知抛物线对称轴为x=1,
∴DG=x-1,DF=![]() (x-1),
(x-1),
∴DE+DF=﹣x2+2x+3+![]() (x-1)=﹣x2+(2+
(x-1)=﹣x2+(2+![]() )x+3-
)x+3-![]() ,
,
∴当x=![]() ,DE+DF有最大值为
,DE+DF有最大值为![]() ;
;

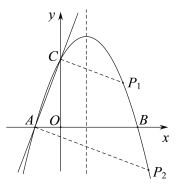
答图1 答图2
(3)①存在;如答图2,过点C作AC的垂线交抛物线于另一点P1,
∵直线AC的解析式为y=3x+3,
∴直线PC的解析式可设为y=![]() x+m,把C(0,3)代入得m=3,
x+m,把C(0,3)代入得m=3,
∴直线P1C的解析式为y=![]() x+3,解方程组
x+3,解方程组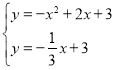 ,解得
,解得![]() 或
或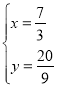 ,则此时P1点坐标为(
,则此时P1点坐标为(![]() ,
,![]() );过点A作AC的垂线交抛物线于另一点P2,直线AP2的解析式可设为y=
);过点A作AC的垂线交抛物线于另一点P2,直线AP2的解析式可设为y=![]() x+n,把A(﹣1,0)代入得n=
x+n,把A(﹣1,0)代入得n=![]() ,
,
∴直线PC的解析式为y=![]() ,解方程组
,解方程组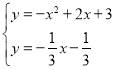 ,解得
,解得![]() 或
或 ,则此时P2点坐标为(
,则此时P2点坐标为(![]() ,
,![]() ),综上所述,符合条件的点P的坐标为(
),综上所述,符合条件的点P的坐标为(![]() ,
,![]() )或(
)或(![]() ,
,![]() );
);
②![]() <t<
<t<![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,已知直线![]() 与
与![]() 相离,
相离,![]() 于点
于点![]() ,
,![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() 与
与![]() 相切于点
相切于点![]() ,
,![]() 的延长线交直线
的延长线交直线![]() 于点
于点![]() .
.
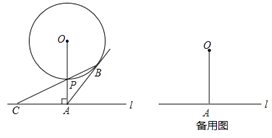
(1)试判断线段![]() 与
与![]() 的数量关系,并说明理由;
的数量关系,并说明理由;
(2)若![]() ,求
,求![]() 的半径和线段
的半径和线段![]() 的长;
的长;
(3)若在![]() 上存在点
上存在点![]() ,使
,使![]() 是以
是以![]() 为底边的等腰三角形,求
为底边的等腰三角形,求![]() 的半径
的半径![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
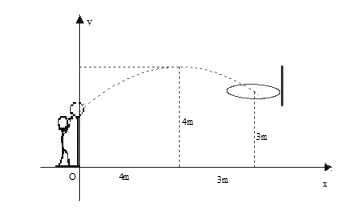
【题目】初三年级的一场篮球比赛中,如图队员甲正在投篮,已知球出手时离地面高![]() m,与篮圈中心的水平距离为7m,当球出手后水平距离为4m时到达最大高度4m,设篮球运行的轨迹为抛物线,篮圈距地面3m.
m,与篮圈中心的水平距离为7m,当球出手后水平距离为4m时到达最大高度4m,设篮球运行的轨迹为抛物线,篮圈距地面3m.
(1)建立如图所示的平面直角坐标系,求抛物线的解析式并判断此球能否准确投中?
(2)此时,若对方队员乙在甲前面1m处跳起盖帽拦截,已知乙的最大摸高为3.1m,那么他能否获得成功?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数G1:y=ax2+bx+c(a≠0)的图象过点(﹣1,0)和(0,3),对称轴为直线x=1.
(1)求二次函数G1的解析式;
(2)当﹣1<x<2时,求函数G1中y的取值范围;
(3)将G1先向右平移3个单位,再向下平移2个单位,得到新二次函数G2,则函数G2的解析式是 .
(4)当直线y=n与G1、G2的图象共有4个公共点时,直接写出n的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)边长分别为5,12,13的三角形内切圆半径是 ;
(2)若四边形ABCD存在内切圆(与各边都相切的圆),如图2且面积为S,各边长分别为a,b,c,d,试推导四边形的内切圆半径公式;
(3)若一个n边形(n为不小于3的整数)存在内切圆,且面积为S,各边长分别为a1,a2,a3,…,an,合理猜想其内切圆半径公式(不需说明理由).

查看答案和解析>>
科目:初中数学 来源: 题型:
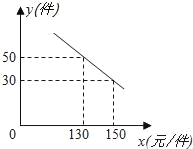
【题目】某商场购进一种每件价格为100元的新商品,在商场试销发现:销售单价x(元/件)与每天销售量y(件)之间满足如图所示的关系:(1)求出y与x之间的函数关系式;(2)如果商店销售这种商品,每天要获得1500元利润,那么每件商品的销售价应定为多少元?(3)写出每天的利润W与销售单价x之间的函数关系式;若你是商场负责人,会将售价定为多少,来保证每天获得的利润最大,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】周末,小华和小亮想用所学的数学知识测量家门前小河的宽.测量时,他们选择了河对岸边的一棵大树,将其底部作为点A,在他们所在的岸边选择了点B,使得AB与河岸垂直,并在B点竖起标杆BC,再在AB的延长线上选择点D竖起标杆DE,使得点E与点C、A共线.
已知:CB⊥AD,ED⊥AD,测得BC=1m,DE=1.5m,BD=8.5m.测量示意图如图所示.请根据相关测量信息,求河宽AB.
查看答案和解析>>
科目:初中数学 来源: 题型:
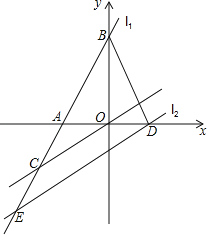
【题目】如图,在平面直角坐标系中,直线l1与x轴交于点A,与y轴交于点B(0,4),OA=![]() OB,点C(﹣3,n)在直线l1上.
OB,点C(﹣3,n)在直线l1上.
(1)求直线l1和直线OC的解析式;
(2)点D是点A关于y轴的对称点,将直线OC沿y轴向下平移,记为l2,若直线l2过点D,与直线l1交于点E,求△BDE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
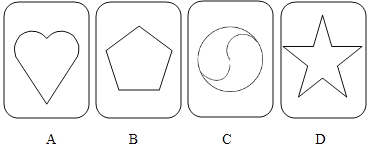
【题目】现有A,B,C,D四张不透明的卡片,除正面上的图案不同外,其他均相同.将这4张卡片背面向上洗匀后放在桌面上.
(Ⅰ)从中随机取出1张卡片,卡片上的图案是中心对称图形的概率是_____;
(Ⅱ)若从中随机抽取一张卡片,不放回,再从剩下的3张中随机抽取1张卡片,请用画树形图或列表的方法,求两次抽取的卡片都是轴对称图形的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com