
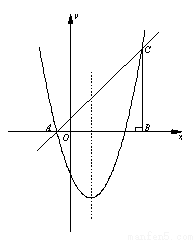
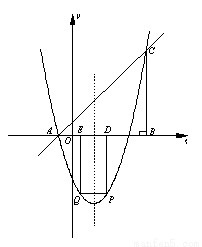
如图,在平面直角坐标系中,△ABC的边AB在x轴上,∠ABC=90°,AB=BC,OA=1,OB=4,抛物线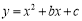 经过A、C两点.
经过A、C两点.
(1)求抛物线的解析式及其顶点坐标;
(2)如图①,点P是抛物线上位于x轴下方的一点,点Q与点P关于抛物线的对称轴对称,过点P、Q分别向x轴作垂线,垂足为点D、E,记矩形DPQE的周长为d,求d的最大值,并求出使d最大值时点P的坐标;
(3)如图②,点M是抛物线上位于直线AC下方的一点,过点M作MF⊥AC于点F,连接MC,作MN∥BC交直线AC于点N,若MN将△MFC的面积分成2:3两部分,请确定M点的坐标.
(1)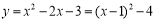 ,(1,-4)
,(1,-4)
【解析】
试题分析:
(1)考查求解抛物线的能力,利用点在抛物线上代入即可得解,再求出顶点坐标.
(2)考查数形结合的能力,利用点在抛物线上,设出P点,写出Q点,得出矩形DPQE的周长为d关于所设变量的函数,再利用二次函数的性质即可得解.
(3)进一步考查数形结合的能力,过点F作FH⊥MN于H,过C作CG⊥MN于G,利用面积比的关系即可得解,注意解值的有意义.
试题解析:
(1)由已知得:A(-1,0)、C(4,5)
∵二次函数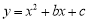 的图像经过点A(-1,0)C(4,5)
的图像经过点A(-1,0)C(4,5)
∴ 解得
解得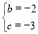
∴抛物线解析式为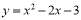
∵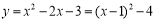
∴顶点坐标为(1,-4)
(2)由(1)知抛物线的对称轴为直线x=1
设点P为((t,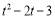 ),
),
∵P、Q为抛物线上的对称点
∴
当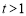 时,
时,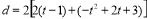
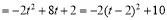
∵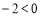
∴当t=2使,d有最大值为10,即点P为(2,-3)
当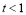 时,由抛物线的轴对称性得,点P为(0,-3)时,d有最大值10
时,由抛物线的轴对称性得,点P为(0,-3)时,d有最大值10
综上,当P为(0,-3)或(2,-3)时,d有最大值10

(3)过点F作FH⊥MN于H,过C作CG⊥MN于G,则∠ANM=∠ACB=45°
∵MF⊥AC
∴ ∴
∴ 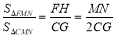
∵A(-1,0),C(4,5)
∴直线AC解析式为y=x+1
设点M为(m, ),其中
),其中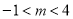 ,则CG=4-m
,则CG=4-m
由MN∥BC得点N为(m,m+1)
∴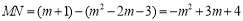
当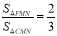 时,有3MN=4CG 即
时,有3MN=4CG 即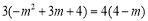
解得: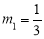
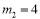 (舍去)
(舍去)
∴点M为
当 时,有2MN=6CG 即
时,有2MN=6CG 即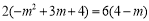
解得: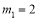
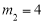 (舍去)
(舍去)
∴点M为(2,-3)
∴ 综上,当M为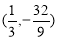 、(2,-3)
、(2,-3)
考点:1.二次函数的性质;2 .数形结合.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源:2014中考名师推荐数学三角形(一)(解析版) 题型:选择题
如图,△ABC中,AB=AC,∠A=36°,BD是AC边上的高,则∠DBC的度数是( )
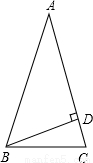
A.18° B.24° C.30° D.36°
查看答案和解析>>
科目:初中数学 来源:2014中考名师推荐数学一元一次不等式组(解析版) 题型:选择题
已知点M(1﹣2m,m﹣1)关于x轴的对称点在第一象限,则m的取值范围在数轴上表示正确的是( )
A.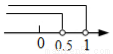
B.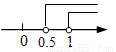
C.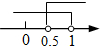
D.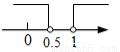
查看答案和解析>>
科目:初中数学 来源:2013-2014学年黑龙江省大庆市九年级下学期期末数学试卷(解析版) 题型:填空题
某商品经过连续两次降价,销售单价由原来的125元降到80元,则平均每次降价的百分率为_____.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年黑龙江省大庆市九年级下学期期末数学试卷(解析版) 题型:选择题
在面积为15的平行四边形ABCD中,过点A作AE垂直于直线BC于点E,作AF垂直于直线CD于点F,若AB=5,BC=6,则CE+CF的值为( )
A.11+ B.11﹣
B.11﹣ C.11+
C.11+ 或11﹣
或11﹣ D.11+
D.11+ 或1+
或1+
查看答案和解析>>
科目:初中数学 来源:2013-2014学年重庆市万州区岩口复兴学校九年级下学期期中命题(一)数学试卷(解析版) 题型:解答题
如图,已知点E、C在线段BF上,BE=CF,AB∥DE,AB=DE.
求证:AC∥DF.

查看答案和解析>>
科目:初中数学 来源:2013-2014学年重庆市万州区岩口复兴学校九年级下学期期中命题(一)数学试卷(解析版) 题型:填空题
《重庆市国民经济和社会发展第十二个五年规划纲要》提出:到2015年,逐步形成西部地区的重要增长极,地区生产总值达到15000亿元.将数据15000亿用科学记数法表示为 亿.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年重庆市万州区岩口复兴学校九年级下学期期中命题四数学试卷(解析版) 题型:解答题
每年3月12日,是中国的植树节。某街道办事处为进一步改善人居环境,准备在街道两边植种行道树,行道树的树种选择取决于居民的喜爱情况.为此,街道办事处的人员随机调查了部分居民,并将结果绘制成如下扇形统计图,其中∠AOB = 126?.
请根据扇形统计图,完成下列问题:
(1)本次调查了多少名居民?其中喜爱香樟的居民有多少人?
(2)请将条形统计图补全(在图中完成).
(3)某中学的一些同学也参与了投票,喜爱“小叶榕”的有四人,其中一名男生;喜爱“黄葛树”的也有四人,其中三名男生.若街道准备分别从这两组中随机选出一名同学参与到街道植树活动中去.请你用列表或画树状图的方法求出所选两名同学恰好是一名女生和一名男生的概率.


查看答案和解析>>
科目:初中数学 来源:2013-2014学年重庆市万州区岩口复兴学校九年级下学期期中命题二数学试卷(解析版) 题型:选择题
某人骑车沿直线旅行,先前进了 千米,休息了一段时间,又原路原速返回了
千米,休息了一段时间,又原路原速返回了 千米(
千米( ),再掉头沿原方向以比原速大的速度行驶,则此人离起点的距离
),再掉头沿原方向以比原速大的速度行驶,则此人离起点的距离 与时间
与时间 的函数关系的大致图象是( ).
的函数关系的大致图象是( ).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com