
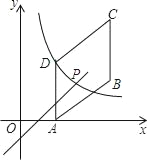
【题目】如图,四边形ABCD是平行四边形,点A(2,0),B(6,2),C(6,6),反比例函数y1=![]() (x>0)的图象过点D,点P是一次函数y2=kx+3﹣3k(k≠0)的图象与该反比例函数的一个公共点,对于下面四个结论:
(x>0)的图象过点D,点P是一次函数y2=kx+3﹣3k(k≠0)的图象与该反比例函数的一个公共点,对于下面四个结论:
①反比例函数的解析式是y1=![]() ;
;
②一次函数y2=kx+3﹣3k(k≠0)的图象一定经过(6,6)点;
③若一次函数y2=kx+3﹣3k的图象经过点C,当x>2![]() 时,y1<y2;
时,y1<y2;
④对于一次函数y2=kx+3﹣3k(k≠0),当y随x的增大而增大时,点P横坐标a的取值范围是0<a<3.
其中正确的是( )
A. ①③ B. ②③ C. ②④ D. ③④
【答案】D
【解析】分析:①根据平行四边形的性质求D点的坐标;(2)把x=6代入y2=kx+3﹣3k中,看函数值是否为6;③把点C的坐标代入y2=kx+3﹣3k,求得一次函数的解析,由一次函数的解析式和反比例函数的解析组成的方程组可求得它们的交点坐标,结合函数图象判断;④一次函数过定点(3,3),确定x=3时的函数值即可.
详解:①∵四边形ABCD是平行四边形,∴AD=BC,
∵B(6,2),C(6,6),∴BC⊥x轴,AD=BC=4,而A点坐标为(2,0),
∴点D的坐标为(2,4),
∵反比例函数y1=![]() (x>0)的函数图象经过点D(2,4),
(x>0)的函数图象经过点D(2,4),
∴4=![]() ,∴m=8,
,∴m=8,
∴反比例函数的解析式为y=![]() ,①不正确;
,①不正确;
②当x=6时,y=kx+3﹣3k=6k+3﹣3k=3k+3≠6,
∴一次函数y=kx+3﹣3k(k≠0)的图象不一定过点C,②不正确;
③∵一次函数y2=kx+3﹣3k的图象经过点C,
∴6=6k+3﹣3k,解得:k=1.
∴y2=x.
联立![]() ,解得:
,解得:![]() 或
或![]() (舍去).
(舍去).
结合函数图象即可得出:
当x>![]() 时,y1<y2,③成立;
时,y1<y2,③成立;
④∵一次函数y2=kx+3﹣3k(k≠0),y随x的增大而增大,
∴k>0,∴交点P在第一象限.
将x=3代入到反比例函数y=![]() 中,得:y=
中,得:y=![]() .
.
∵因为y2-3=k(x﹣3),当x=3时,y2=3,
∴一次函数y2=kx+3﹣3k(k≠0)恒过点(3,3),点(3,![]() )在(3,3)的下方,
)在(3,3)的下方,
即点P应该在点(3,![]() )的左方,∴点P横坐标a的取值范围是a<3.
)的左方,∴点P横坐标a的取值范围是a<3.
即④正确.
综上可知:③④正确,
故选D.


科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C在⊙O上,∠ABC的平分线与AC相交于点D,与⊙O过点A的切线相交于点E.
(1)∠ACB= °,理由是: ;
(2)猜想△EAD的形状,并证明你的猜想;
(3)若AB=8,AD=6,求BD.

查看答案和解析>>
科目:初中数学 来源: 题型:
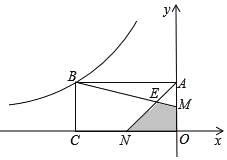
【题目】如图,矩形OABC的两边OA、OC在坐标轴上,且OC=2OA,M、N分别为OA、OC的中点,BM与AN交于点E,若四边形EMON的面积为2,则经过点B的双曲线的解析式为( )
A. y=﹣![]() B. y=﹣
B. y=﹣![]() C. y=﹣
C. y=﹣![]() D. y=﹣
D. y=﹣![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知平面直角坐标系中两定点A(﹣1,0)、B(4,0),抛物线y=ax2+bx﹣2(a≠0)过点A,B,顶点为C,点P(m,n)(n<0)为抛物线上一点.
(1)求抛物线的解析式和顶点C的坐标;
(2)当∠APB为钝角时,求m的取值范围;
(3)若m>![]() ,当∠APB为直角时,将该抛物线向左或向右平移t(0<t<
,当∠APB为直角时,将该抛物线向左或向右平移t(0<t<![]() )个单位,点C、P平移后对应的点分别记为C′、P′,是否存在t,使得首位依次连接A、B、P′、C′所构成的多边形的周长最短?若存在,求t的值并说明抛物线平移的方向;若不存在,请说明理由.
)个单位,点C、P平移后对应的点分别记为C′、P′,是否存在t,使得首位依次连接A、B、P′、C′所构成的多边形的周长最短?若存在,求t的值并说明抛物线平移的方向;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】重庆市江津区是中国著名的“花椒之乡”,其地理气候条件优越,所产花椒麻香味浓, 并且富含多种微量元素,出油率高,不仅是优良的调味品,而且经加工,可提取多种名贵的化工原料.去年江津某村积极改革农村产业结构,增加农名收入,村委会多方筹集资金,流转耕地 1200 亩,全都用于种植大红袍花椒和九叶青花椒两个品种,花椒上市后,大红袍花椒每
亩获利 1000 元,九叶青花椒每亩获利 1200 元.
(1)去年该村种植的1200亩花椒,至少获利128万元,则该村种植大红花胶的面积最多为多少亩?
(2)今年村里保持(1)中大红袍花椒的最多面积种植大红袍花椒,且每亩的获利比去年增加![]() a%;由于九叶青花椒每亩获利较多,村里利用新增流转耕地,使九叶青花椒的种植面积,在去年最少种植面积的基础上扩大2a%,同时每亩利润将增加
a%;由于九叶青花椒每亩获利较多,村里利用新增流转耕地,使九叶青花椒的种植面积,在去年最少种植面积的基础上扩大2a%,同时每亩利润将增加![]() a%,这样今年花椒的总利润达到了208万元,求a的值.
a%,这样今年花椒的总利润达到了208万元,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
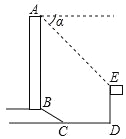
【题目】如图所示,某办公大楼正前方有一根高度是15米的旗杆ED,从办公大楼顶端A测得旗杆顶端E的俯角α是45°,旗杆低端D到大楼前梯砍底边的距离DC是20米,梯坎坡长BC是12米,梯坎坡度i=1:![]() ,则大楼AB的高度为_________米.
,则大楼AB的高度为_________米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在正方形ABCD中,E为CD边上的一点,F为BC的延长线上一点,CE=CF。
⑴△BCE与△DCF全等吗?说明理由;
⑵若∠BEC=60o,求∠EFD。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A的坐标为(﹣![]() ,0),点B的坐标为(0,3).
,0),点B的坐标为(0,3).
(1)求过A,B两点直线的函数表达式;
(2)过B点作直线BP与x轴交于点P,且使OP=2OA,求△ABP的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
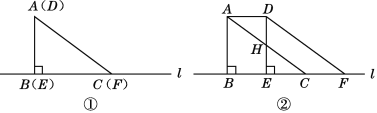
【题目】两个全等的直角三角形重叠放在直线l上,如图①所示,AB=6 cm,AC=10 cm,∠ABC=90°,将Rt△ABC在直线l上左右平移(如图②).
(1)求证:四边形ACFD是平行四边形.
(2)怎样移动Rt△ABC,使得四边形ACFD的面积等于△ABC的面积的一半?
(3)将Rt△ABC向左平移4 cm,求四边形DHCF的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com