
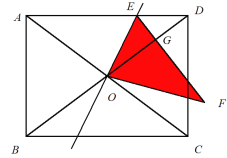
【题目】如图,矩形ABCD中,AB=3,BC=4,对角线AC,BD相交于点O,点E是AD边上一动点,将△AEO沿直线EO折叠,点A落在点F处,线段EF,OD相交于点G.若△DEG是直角三角形,则线段DE的长为____________
【答案】![]() 或
或![]() .
.
【解析】
分情况讨论:当∠EGD=90°时,设DE=x,先利用勾股定理求得AC=BD=5,进而可求得tan∠ADB=![]() ,sin∠GFO=
,sin∠GFO=![]() ,cos∠ADB=
,cos∠ADB=![]() ,进而表示出DG=
,进而表示出DG=![]() x,OG=OD-DG=
x,OG=OD-DG=![]() -
-![]() x,最后根据sin∠GFO=
x,最后根据sin∠GFO=![]() 列出方程求解即可;当∠GED=90°时,则由折叠知,∠AEO=∠OEF=45°,过点O作OH⊥AD于H,设DE=x,则EH=HD-DE=2-x,再根据tan∠ADO=
列出方程求解即可;当∠GED=90°时,则由折叠知,∠AEO=∠OEF=45°,过点O作OH⊥AD于H,设DE=x,则EH=HD-DE=2-x,再根据tan∠ADO=![]() 列出方程求解即可.
列出方程求解即可.
(1)当∠EGD=90°时,如图,设DE=x,
∵在矩形ABCD中,AB=3,BC=4,∠ABC=∠BAD=∠ADC=90°,
∴AC=BD=![]() ,AD=BC=4,CD=AB=3,
,AD=BC=4,CD=AB=3,
∴OA=OD=![]() BD=
BD=![]() ,
,
∵将△AEO沿直线EO折叠,点A落在点F处,
∴OF=OA=![]() ,∠DAC=∠F,
,∠DAC=∠F,
∴在Rt△ABD中,tan∠ADB=![]() ,
,
同理可得:sin∠GFO=![]() ,cos∠ADB=
,cos∠ADB=![]() ,
,
∵在Rt△DEG中,cos∠EDG=![]()
∴DG=![]() x,
x,
∴OG=OD-DG=![]() -
-![]() x,
x,
∵在Rt△OGF中,sin∠GFO=![]()
∴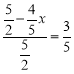 ,
,
解得:x=![]() ;
;
(2)当∠GED=90°时,
则由折叠知,∠AEO=∠OEF=45°,
过点O作OH⊥AD于H,如图所示,
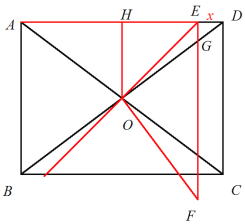
∴△EHO为等腰直角三角形,HE=HO,
∵OA=OD,OH⊥AD,
∴HD=![]() AD=2,
AD=2,
设DE=x,则EH=HD-DE=2-x,
∴OH=EH=2-x,
∵tan∠ADO=![]() ,
,
∴![]() ,
,
解得:x=![]() ;
;
∴综上所述,DE的长为![]() 或
或![]() .
.
故答案为:![]() 或
或![]() .
.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案科目:初中数学 来源: 题型:
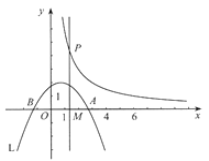
【题目】如图,抛物线L: ![]() (常数t>0)与x轴从左到右的交点为B,A,过线段OA的中点M作MP⊥x轴,交双曲线
(常数t>0)与x轴从左到右的交点为B,A,过线段OA的中点M作MP⊥x轴,交双曲线![]() 于点P,且OA·MP=12.
于点P,且OA·MP=12.
(1)求k值;
(2)当t=1时,求AB长,并求直线MP与L对称轴之间的距离;
(3)把L在直线MP左侧部分的图象(含与直线MP的交点)记为G,用t表示图象G最高点的坐标;
(4)设L与双曲线有个交点的横坐标为x0,且满足4≤x0≤6,通过L位置随t变化的过程,直接写出t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某报社为了解温州市民对大范围雾霾天气的成因、影响以及应对措施的看法,做了一次抽样调查,调查结果共分为四个等级:A.非常了解:B.比较了解:C.基本了解;D.不了解.根据调查统计结果,绘制了不完整的三种统计图表.请结合统计图表,回答下列问题:
对雾霾的了解程度 | 百分比 | |
A | 非常了解 | 5% |
B | 比较了解 | m% |
C | 基本了解 | 45% |
D | 不了解 | n% |
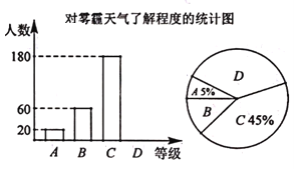
(1)本次参与调查的市民共有________人,m=________,n=________.
(2)统计图中扇形D的圆心角是________度.
(3)某校准备开展关于雾霾的知识竞赛,九(3)班郑老师欲从2名男生和1名女生中任选2人参加比赛,求恰好选中“1男1女”的概率(要求列表或画树状图).
查看答案和解析>>
科目:初中数学 来源: 题型:
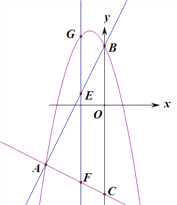
【题目】如图,抛物线y=-x2+bx+c与直线AB交于A(-4,-4),B(0,4)两点,直线AC:y=-![]() x-6交y轴与点C.点E是直线AB上的动点,过点E作EF⊥x轴交AC于点F,交抛物线于点G.
x-6交y轴与点C.点E是直线AB上的动点,过点E作EF⊥x轴交AC于点F,交抛物线于点G.
(1)求抛物线y=-x2+bx+c的表达式;
(2)连接GB、EO,当四边形GEOB是平行四边形时,求点G的坐标;
(3)①在y轴上存在一点H,连接EH、HF,当点E运动到什么位置时,以A、E、F、H为顶点的四边形是矩形?求出此时点E、H的坐标;
②在①的前提下,以点E为圆心,EH长为半径作圆,点M为⊙E上一动点,求![]() AM+CM的最小值.
AM+CM的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某宝网店销售甲、乙两种电器,已知甲种电器每个的售价比乙种电器多60元,马老师从该网店购买了3个甲种电器和2个乙种电器,共花费780元.
(1)该店甲、乙两种电器每个的售价各是多少元?
(2)根据销售情况,店主决定用不少于10800元的资金购进甲、乙两种电器,这两种电器共100个,已知甲种电器每个的进价为150元,乙种电器每个的进价为80元.若所购进电器均可全部售出,请求出网店所获利润W(元)与甲种电器进货量m(个)之间的函数关系式,并说明当m为何值时所获利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
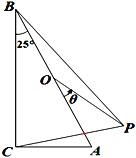
【题目】如图,在△ABC中,∠ACB=90°,∠ABC=25°,O为AB的中点. 将OA绕点O逆时针旋转θ °至OP(0<θ<180),当△BCP恰为轴对称图形时,θ的值为_____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为更好地践行社会主义核心价值观,让同学们珍惜粮食,学会感恩.校学生会积极倡导“光盘行动”,某天午餐后学生会干部随机调查了部分同学就餐饭菜的剩余情况,并将结果统计后制成如图所示的不完整的统计图.
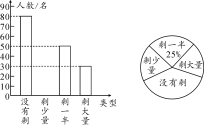
(1)这次被调查的同学共有________名;
(2)计算在扇形统计图中剩大量饭菜所对应扇形圆心角的度数;
(3)校学生会通过数据分析,估计这次被调查的所有学生一餐浪费的食物可以提供40人用餐.据此估算,全校2000名学生一餐浪费的食物可供多少人食用一餐?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】作图题:如图在矩形ABCD中,已知AD=10,AB=6,用直尺和圆规在AD上找一点E(保留作图痕迹),使EC平分∠BED,并求出tan∠BEC的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com