
【题目】某宝网店销售甲、乙两种电器,已知甲种电器每个的售价比乙种电器多60元,马老师从该网店购买了3个甲种电器和2个乙种电器,共花费780元.
(1)该店甲、乙两种电器每个的售价各是多少元?
(2)根据销售情况,店主决定用不少于10800元的资金购进甲、乙两种电器,这两种电器共100个,已知甲种电器每个的进价为150元,乙种电器每个的进价为80元.若所购进电器均可全部售出,请求出网店所获利润W(元)与甲种电器进货量m(个)之间的函数关系式,并说明当m为何值时所获利润最大?最大利润是多少?
【答案】(1)甲、乙两种电器每个的售价各是180元、120元;(2)当m=40时,W取最大值,最大利润为:3600元.
【解析】
(1)设甲、乙两种电器每个的售价各是x元、y元,根据式子列出方程组,求出结果就可以
(2)根据利润=单个利润×数量,再由总利润=甲的利润+乙的利润,列出等式即可
(1)设甲、乙两种电器每个的售价各是x元、y元
∴![]() ,解得:
,解得:![]() ,
,
答:甲、乙两种电器每个的售价各是180元、120元
(2)由题意得:W=(180-150)m+(120-80)(100-m)=4000-10m
由题意得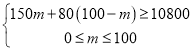 ,解得:40≤m≤100,
,解得:40≤m≤100,
由W==4000-10m知,W随m的增大而减小,
∴当m=40时,W取最大值,最大利润为:3600元.


科目:初中数学 来源: 题型:
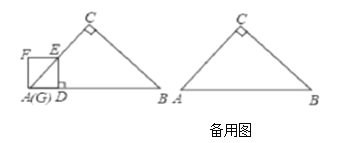
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,线段
,线段![]() 上一动点
上一动点![]() ,以
,以![]() 的速度从点
的速度从点![]() 出发向终点
出发向终点![]() 运动.过点
运动.过点![]() 作
作![]() ,交折线
,交折线![]() 于点
于点![]() ,以
,以![]() 为一边,在
为一边,在![]() 左侧作正方形
左侧作正方形![]() .设运动时间为
.设运动时间为![]()
![]() ,正方形
,正方形![]() 与
与![]() 重叠部分面积为
重叠部分面积为![]() .
.
(1)![]() ________
________![]() ;
;
(2)当![]() 为何值时,点
为何值时,点![]() 在
在![]() 上;
上;
(3)求![]() 与
与![]() 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
(4)直线![]() 将
将![]() 面积分成
面积分成![]() 两部分时,直接写出
两部分时,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
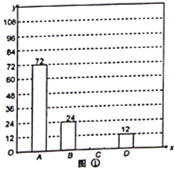
【题目】马山被誉为“中国民间文化艺术之乡”,马山的民族文化丰富多彩,形式多样.为了了解某学学生对马山民族文化的喜爱情况,某校开展了“我最喜爱的民俗活动”调查问卷,其中包括:![]() 壮族三声部民歌,
壮族三声部民歌,![]() 壮族扁担舞,
壮族扁担舞,![]() 会鼓,
会鼓,![]() 采茶舞.将调查问卷结果收集整理后,绘制了以下不完整的条形统计图(图①)和扇形统计图(图②),根据图中所提供的信息解答下列问题:
采茶舞.将调查问卷结果收集整理后,绘制了以下不完整的条形统计图(图①)和扇形统计图(图②),根据图中所提供的信息解答下列问题:
(1)这次抽样调查中,一共抽查了名学生,![]() 项所对应圆心角的度数为;
项所对应圆心角的度数为;
(2)请补全条形统计图;
(3)若九(1)班要从甲、乙、丙和丁这四人中选两个人参与调查,请用列表法或画树状图法求出恰好选中甲乙的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
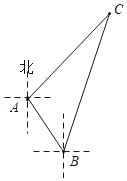
【题目】如图,某考察船在某海域进行科考活动,在点A测得小岛C在它的东北方向上,它沿南偏东37°方向航行了2海里到达点B处,又测得小岛C在它的北偏东23°方向上.
(1)求∠C的度数;
(2)求该考察船在点B处与小岛C之间的距离.(精确到0.1海里)
(参考数据:sin22°≈0.37,cos22°≈0.93,tan22°≈0.40,![]() =1.41,
=1.41,![]() =1.73)
=1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=3,BC=4,对角线AC,BD相交于点O,点E是AD边上一动点,将△AEO沿直线EO折叠,点A落在点F处,线段EF,OD相交于点G.若△DEG是直角三角形,则线段DE的长为____________
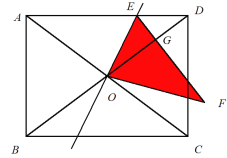
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形纸片![]() 的边长为
的边长为![]() ,翻折
,翻折![]() ,使两个直角顶点重合于对角线
,使两个直角顶点重合于对角线![]() 上一点
上一点![]() 分别是折痕,设
分别是折痕,设![]() ,给出下列判断:
,给出下列判断:
①当![]() 时,点
时,点![]() 是正方形
是正方形![]() 的中心;
的中心;
②当![]() 时,
时,![]() ;
;
③当![]() 时,六边形
时,六边形![]() 面积的最大值是
面积的最大值是![]()
④当![]() 时,六边形
时,六边形![]() 周长的值不变.
周长的值不变.
其中错误的是( )
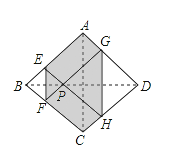
A.②③B.③④C.①④D.①②
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】山地自行车越来越受到中学生的喜爱,各种品牌相继投放市场,某车行经营的A型车去年销售总额为5万元,今年每辆销售价比去年降低400元,若卖出的数量相同,销售总额将比去年减少20%.
(1)今年A型车每辆售价多少元?(列方程解答)
(2)该车行计划今年新进一批A型车和B型车共60辆,A型车的进货价为每辆1100元,销售价与(1)相同;B型车的进货价为每辆1400元,销售价为每辆2000元,且B型车的进货数量不超过A型车数量的两倍,应如何进货才能使这批车获利最多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,抛物线y=ax2+bx+c(a≠0)的顶点为A(s,t)(其中s≠0).
(1)若抛物线经过(2,7)和(-3,37)两点,且s=1.
①求抛物线的解析式;
②若n>1,设点M(n,y1),N(n+1,y2)在抛物线上,比较y1,y2的大小关系,并说明理由;
(2)若a=2,c=-2,直线y=2x+m与抛物线y=ax2+bx+c的交于点P和点Q,点P的横坐标为h,点Q的横坐标为h+3,求出b和h的函数关系式;
(3)若点A在抛物线y=![]() 上,且2≤s<3时,求a的取值范围.
上,且2≤s<3时,求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com